
Question Number 193750 by thean last updated on 19/Jun/23
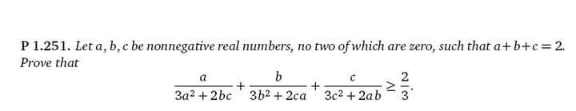
Answered by Subhi last updated on 19/Jun/23
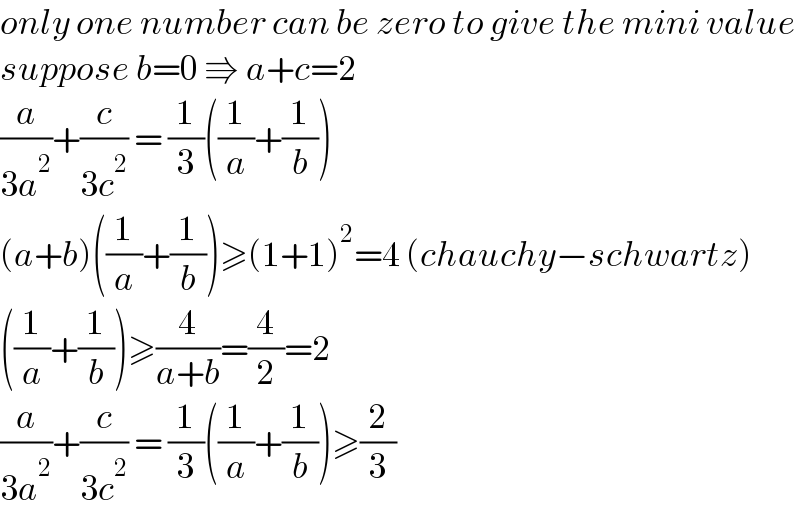
$${only}\:{one}\:{number}\:{can}\:{be}\:{zero}\:{to}\:{give}\:{the}\:{mini}\:{value} \\ $$$${suppose}\:{b}=\mathrm{0}\:\Rrightarrow\:{a}+{c}=\mathrm{2} \\ $$$$\frac{{a}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{{c}}{\mathrm{3}{c}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right) \\ $$$$\left({a}+{b}\right)\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right)\geqslant\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\:\left({chauchy}−{schwartz}\right) \\ $$$$\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right)\geqslant\frac{\mathrm{4}}{{a}+{b}}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$$$\frac{{a}}{\mathrm{3}{a}^{\mathrm{2}} }+\frac{{c}}{\mathrm{3}{c}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}\right)\geqslant\frac{\mathrm{2}}{\mathrm{3}} \\ $$
