
Question Number 193749 by Mingma last updated on 19/Jun/23
Answered by som(math1967) last updated on 19/Jun/23
Commented by som(math1967) last updated on 19/Jun/23
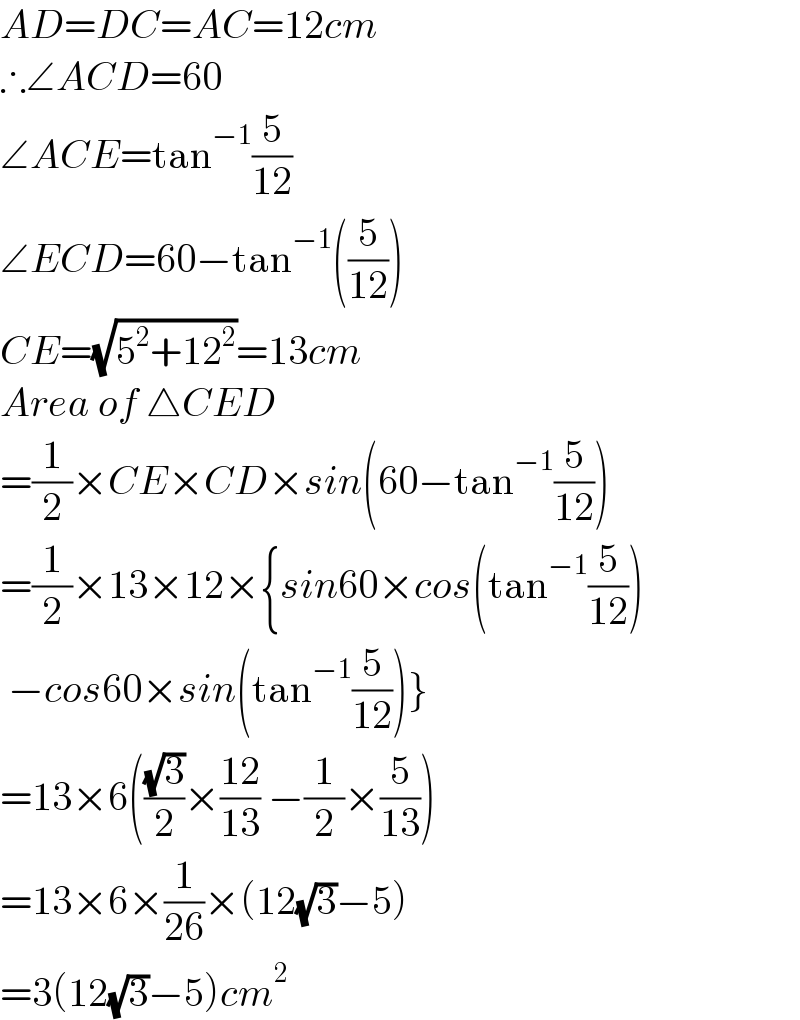
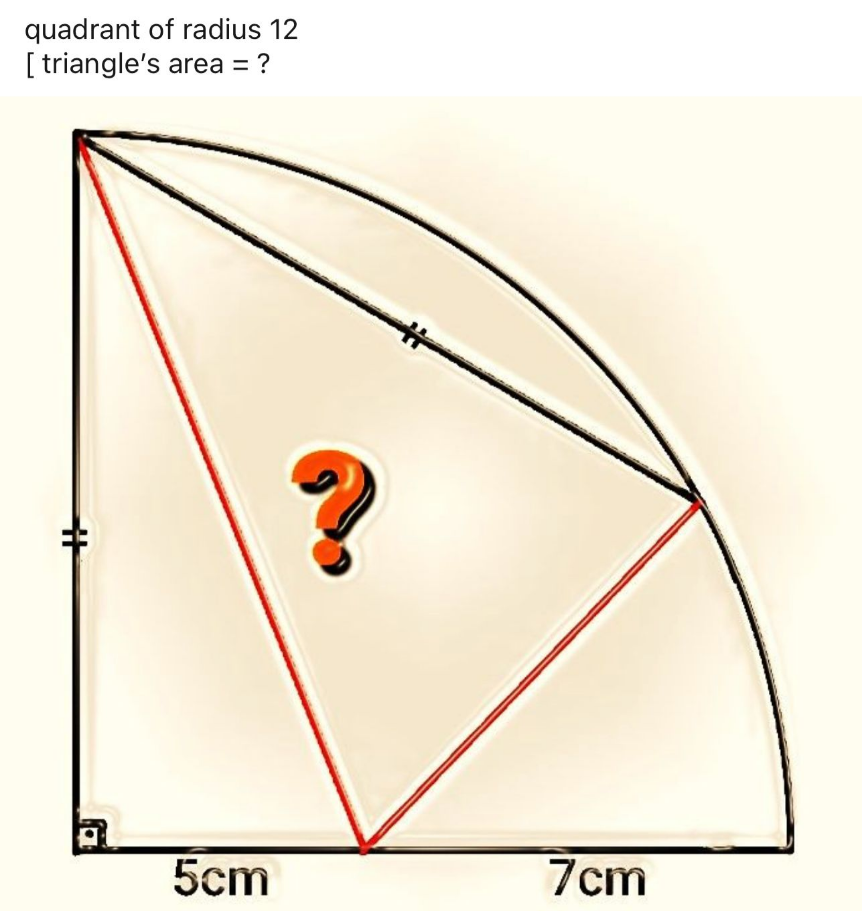
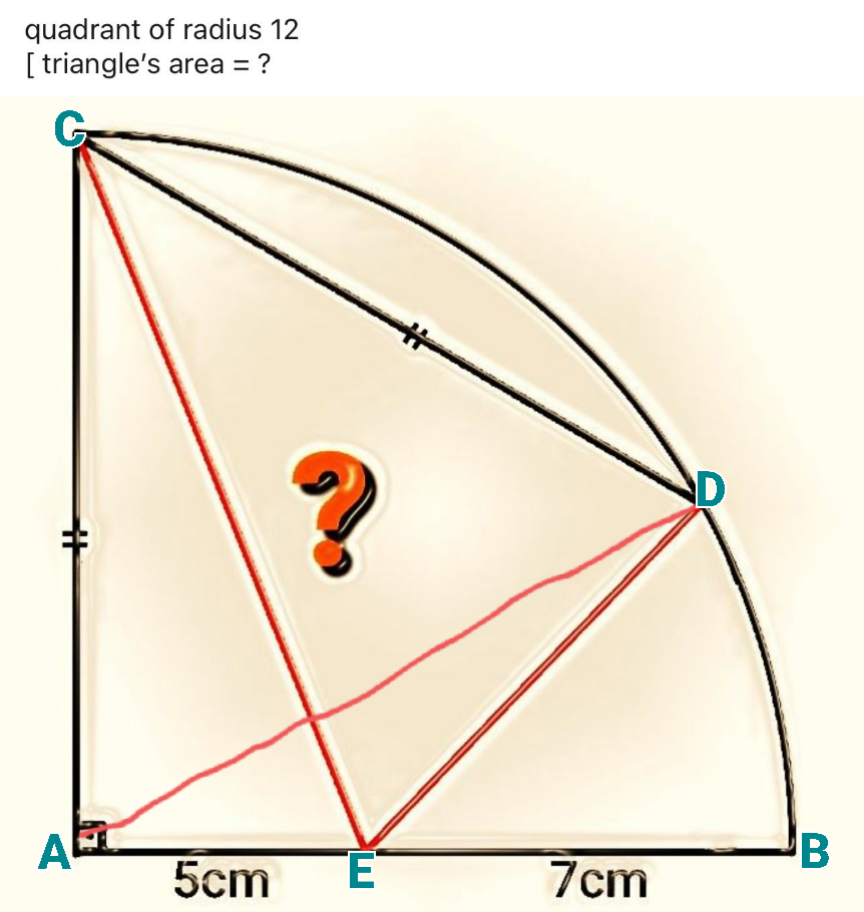
$${AD}={DC}={AC}=\mathrm{12}{cm} \\ $$$$\therefore\angle{ACD}=\mathrm{60} \\ $$$$\angle{ACE}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\angle{ECD}=\mathrm{60}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{12}}\right) \\ $$$${CE}=\sqrt{\mathrm{5}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\mathrm{13}{cm} \\ $$$${Area}\:{of}\:\bigtriangleup{CED} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×{CE}×{CD}×{sin}\left(\mathrm{60}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{12}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{13}×\mathrm{12}×\left\{{sin}\mathrm{60}×{cos}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{12}}\right)\right. \\ $$$$\left.\:−{cos}\mathrm{60}×{sin}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{5}}{\mathrm{12}}\right)\right\} \\ $$$$=\mathrm{13}×\mathrm{6}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{12}}{\mathrm{13}}\:−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{5}}{\mathrm{13}}\right) \\ $$$$=\mathrm{13}×\mathrm{6}×\frac{\mathrm{1}}{\mathrm{26}}×\left(\mathrm{12}\sqrt{\mathrm{3}}−\mathrm{5}\right) \\ $$$$=\mathrm{3}\left(\mathrm{12}\sqrt{\mathrm{3}}−\mathrm{5}\right){cm}^{\mathrm{2}} \\ $$
Commented by Mingma last updated on 19/Jun/23
Perfect ��
