
Question Number 193721 by sciencestudentW last updated on 18/Jun/23
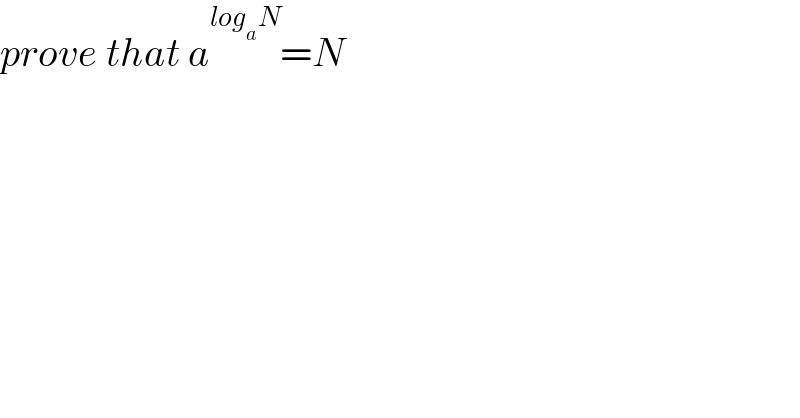
$${prove}\:{that}\:{a}^{{log}_{{a}} {N}} ={N} \\ $$
Answered by MATHEMATICSAM last updated on 18/Jun/23
![From log definition we know if a^x = N then we can write it as x = log_a N a^x = N ⇒ a^(log_a N) = N [∵ x = log_a N]](Q193725.png)
$$\mathrm{From}\:\mathrm{log}\:\mathrm{definition}\:\mathrm{we}\:\mathrm{know}\:\mathrm{if} \\ $$$${a}^{{x}} \:=\:{N}\:\mathrm{then}\:\mathrm{we}\:\mathrm{can}\:\mathrm{write}\:\mathrm{it}\:\mathrm{as} \\ $$$${x}\:=\:\mathrm{log}_{{a}} {N} \\ $$$${a}^{{x}} \:=\:{N} \\ $$$$\Rightarrow\:{a}^{\mathrm{log}_{{a}} {N}} \:=\:{N}\:\left[\because\:{x}\:=\:\mathrm{log}_{{a}} {N}\right] \\ $$
Answered by mr W last updated on 18/Jun/23
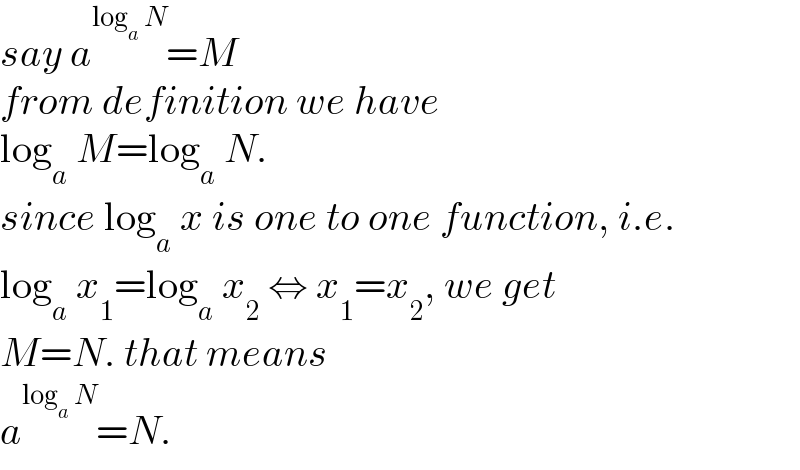
$${say}\:{a}^{\mathrm{log}_{{a}} \:{N}} ={M} \\ $$$${from}\:{definition}\:{we}\:{have} \\ $$$$\mathrm{log}_{{a}} \:{M}=\mathrm{log}_{{a}} \:{N}. \\ $$$${since}\:\mathrm{log}_{{a}} \:{x}\:{is}\:{one}\:{to}\:{one}\:{function},\:{i}.{e}. \\ $$$$\mathrm{log}_{{a}} \:{x}_{\mathrm{1}} =\mathrm{log}_{{a}} \:{x}_{\mathrm{2}} \:\Leftrightarrow\:{x}_{\mathrm{1}} ={x}_{\mathrm{2}} ,\:{we}\:{get} \\ $$$${M}={N}.\:{that}\:{means} \\ $$$${a}^{\mathrm{log}_{{a}} \:{N}} ={N}. \\ $$
Answered by JDamian last updated on 18/Jun/23
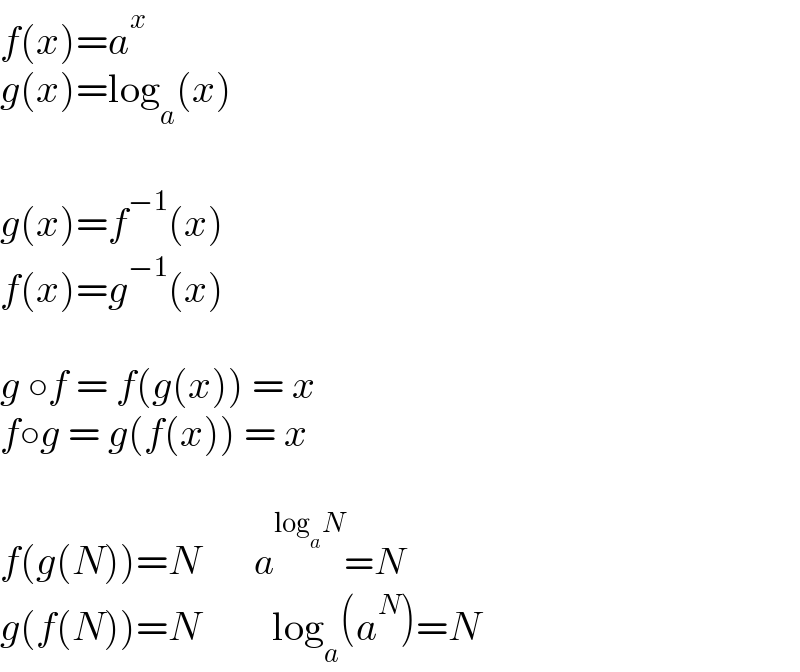
$${f}\left({x}\right)={a}^{{x}} \\ $$$${g}\left({x}\right)=\mathrm{log}_{{a}} \left({x}\right) \\ $$$$ \\ $$$${g}\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right) \\ $$$${f}\left({x}\right)={g}^{−\mathrm{1}} \left({x}\right) \\ $$$$ \\ $$$${g}\:\circ{f}\:=\:{f}\left({g}\left({x}\right)\right)\:=\:{x} \\ $$$${f}\circ{g}\:=\:{g}\left({f}\left({x}\right)\right)\:=\:{x} \\ $$$$ \\ $$$${f}\left({g}\left({N}\right)\right)={N}\:\:\:\:\:\:\:\:\:{a}^{\mathrm{log}_{{a}} {N}} ={N} \\ $$$${g}\left({f}\left({N}\right)\right)={N}\:\:\:\:\:\:\:\:\:\mathrm{log}_{{a}} \left({a}^{{N}} \right)={N} \\ $$
