Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 193533 by horsebrand11 last updated on 16/Jun/23

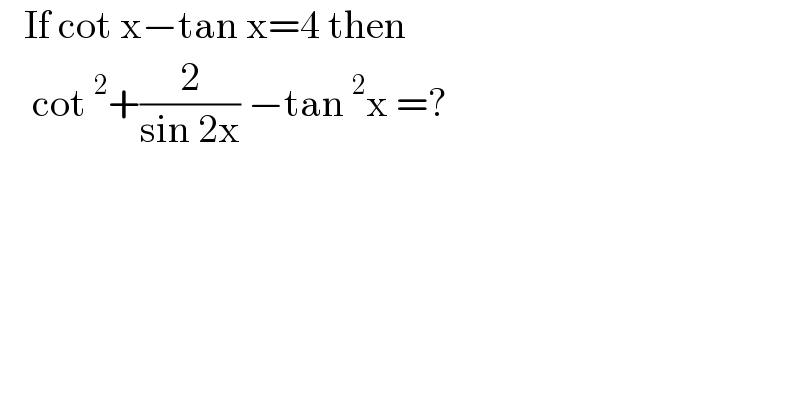
If cot x−tan x=4 then cot^2 +(2/(sin 2x)) −tan^2 x =?

$$\:\:\:\mathrm{If}\:\mathrm{cot}\:\mathrm{x}−\mathrm{tan}\:\mathrm{x}=\mathrm{4}\:\mathrm{then} \\ $$$$\:\:\:\:\mathrm{cot}\:^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{2x}}\:−\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}\:=? \\ $$

Answered by MM42 last updated on 16/Jun/23

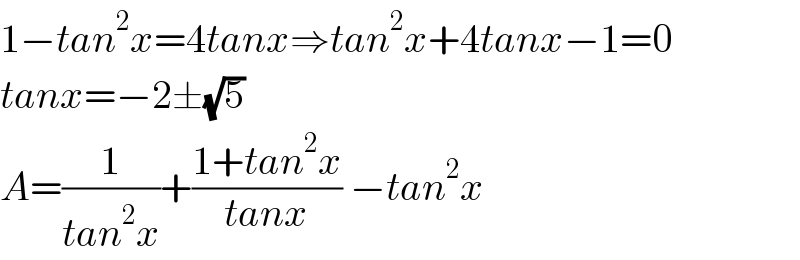
1−tan^2 x=4tanx⇒tan^2 x+4tanx−1=0 tanx=−2±(√5) A=(1/(tan^2 x))+((1+tan^2 x)/(tanx)) −tan^2 x

$$\mathrm{1}−{tan}^{\mathrm{2}} {x}=\mathrm{4}{tanx}\Rightarrow{tan}^{\mathrm{2}} {x}+\mathrm{4}{tanx}−\mathrm{1}=\mathrm{0} \\ $$$${tanx}=−\mathrm{2}\pm\sqrt{\mathrm{5}} \\ $$$${A}=\frac{\mathrm{1}}{{tan}^{\mathrm{2}} {x}}+\frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}}{{tanx}}\:−{tan}^{\mathrm{2}} {x} \\ $$

Answered by Rajpurohith last updated on 19/Jun/23

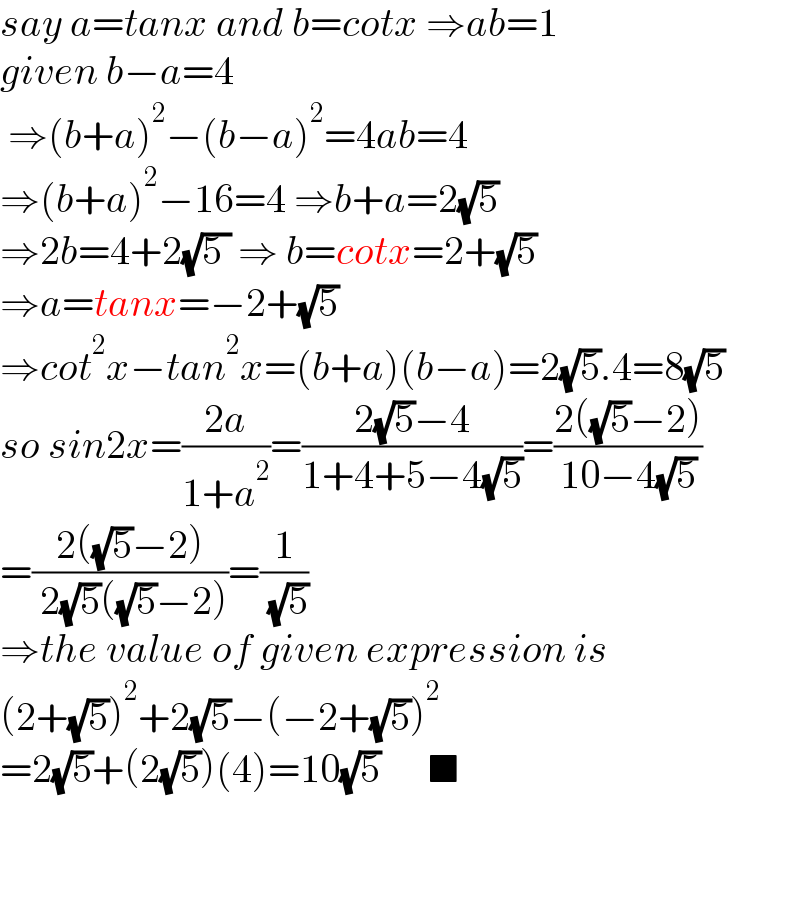
say a=tanx and b=cotx ⇒ab=1 given b−a=4 ⇒(b+a)^2 −(b−a)^2 =4ab=4 ⇒(b+a)^2 −16=4 ⇒b+a=2(√5) ⇒2b=4+2(√(5 )) ⇒ b=cotx=2+(√5) ⇒a=tanx=−2+(√5) ⇒cot^2 x−tan^2 x=(b+a)(b−a)=2(√5).4=8(√5) so sin2x=((2a)/(1+a^2 ))=((2(√5)−4)/(1+4+5−4(√5)))=((2((√5)−2))/(10−4(√5))) =((2((√5)−2))/( 2(√5)((√5)−2)))=(1/( (√5))) ⇒the value of given expression is (2+(√5))^2 +2(√5)−(−2+(√5))^2 =2(√5)+(2(√5))(4)=10(√5) ■

$${say}\:{a}={tanx}\:{and}\:{b}={cotx}\:\Rightarrow{ab}=\mathrm{1} \\ $$$${given}\:{b}−{a}=\mathrm{4} \\ $$$$\:\Rightarrow\left({b}+{a}\right)^{\mathrm{2}} −\left({b}−{a}\right)^{\mathrm{2}} =\mathrm{4}{ab}=\mathrm{4} \\ $$$$\Rightarrow\left({b}+{a}\right)^{\mathrm{2}} −\mathrm{16}=\mathrm{4}\:\Rightarrow{b}+{a}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{2}{b}=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{5}\:}\:\Rightarrow\:{b}={cotx}=\mathrm{2}+\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{a}={tanx}=−\mathrm{2}+\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{cot}^{\mathrm{2}} {x}−{tan}^{\mathrm{2}} {x}=\left({b}+{a}\right)\left({b}−{a}\right)=\mathrm{2}\sqrt{\mathrm{5}}.\mathrm{4}=\mathrm{8}\sqrt{\mathrm{5}} \\ $$$${so}\:{sin}\mathrm{2}{x}=\frac{\mathrm{2}{a}}{\mathrm{1}+{a}^{\mathrm{2}} }=\frac{\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{4}}{\mathrm{1}+\mathrm{4}+\mathrm{5}−\mathrm{4}\sqrt{\mathrm{5}}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)}{\mathrm{10}−\mathrm{4}\sqrt{\mathrm{5}}} \\ $$$$=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)}{\:\mathrm{2}\sqrt{\mathrm{5}}\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow{the}\:{value}\:{of}\:{given}\:{expression}\:{is} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{5}}−\left(−\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{5}}+\left(\mathrm{2}\sqrt{\mathrm{5}}\right)\left(\mathrm{4}\right)=\mathrm{10}\sqrt{\mathrm{5}}\:\:\:\:\:\:\blacksquare \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com