
Question Number 19329 by Tinkutara last updated on 09/Aug/17
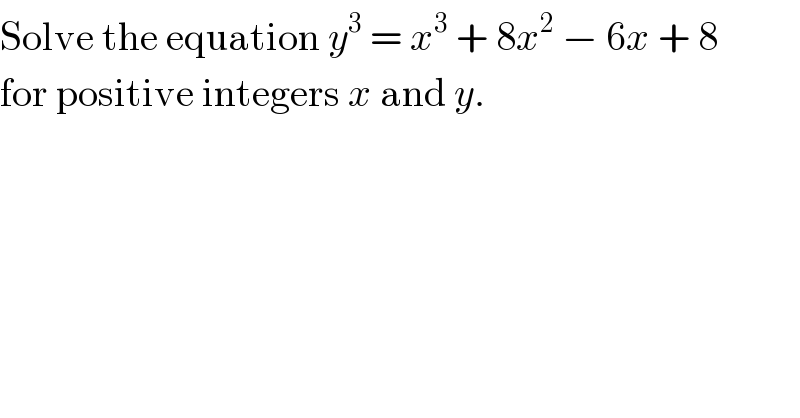
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}\:{y}^{\mathrm{3}} \:=\:{x}^{\mathrm{3}} \:+\:\mathrm{8}{x}^{\mathrm{2}} \:−\:\mathrm{6}{x}\:+\:\mathrm{8} \\ $$$$\mathrm{for}\:\mathrm{positive}\:\mathrm{integers}\:{x}\:\mathrm{and}\:{y}. \\ $$
Commented by Tinkutara last updated on 12/Aug/17

$$\mathrm{RMO}\:\mathrm{2000} \\ $$
Commented by Tinkutara last updated on 12/Aug/17

$$\mathrm{help}\:\mathrm{pls} \\ $$
Commented by Tinkutara last updated on 12/Aug/17
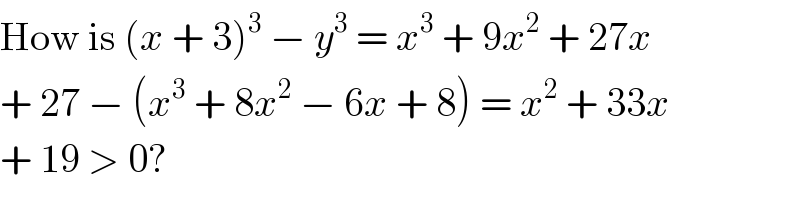
$$\mathrm{How}\:\mathrm{is}\:\left({x}\:+\:\mathrm{3}\right)^{\mathrm{3}} \:−\:{y}^{\mathrm{3}} \:=\:{x}^{\mathrm{3}} \:+\:\mathrm{9}{x}^{\mathrm{2}} \:+\:\mathrm{27}{x} \\ $$$$+\:\mathrm{27}\:−\:\left({x}^{\mathrm{3}} \:+\:\mathrm{8}{x}^{\mathrm{2}} \:−\:\mathrm{6}{x}\:+\:\mathrm{8}\right)\:=\:{x}^{\mathrm{2}} \:+\:\mathrm{33}{x} \\ $$$$+\:\mathrm{19}\:>\:\mathrm{0}? \\ $$
Commented by ajfour last updated on 12/Aug/17
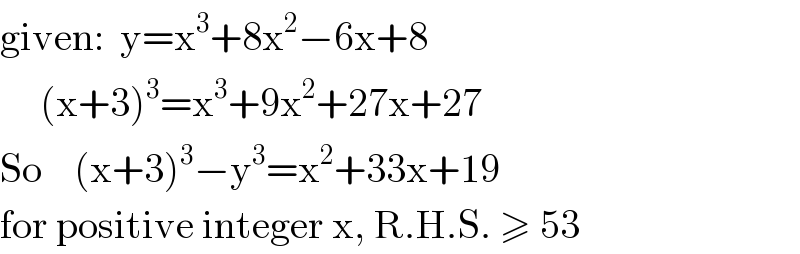
$$\mathrm{given}:\:\:\mathrm{y}=\mathrm{x}^{\mathrm{3}} +\mathrm{8x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{8} \\ $$$$\:\:\:\:\:\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{3}} =\mathrm{x}^{\mathrm{3}} +\mathrm{9x}^{\mathrm{2}} +\mathrm{27x}+\mathrm{27} \\ $$$$\mathrm{So}\:\:\:\:\left(\mathrm{x}+\mathrm{3}\right)^{\mathrm{3}} −\mathrm{y}^{\mathrm{3}} =\mathrm{x}^{\mathrm{2}} +\mathrm{33x}+\mathrm{19} \\ $$$$\mathrm{for}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{x},\:\mathrm{R}.\mathrm{H}.\mathrm{S}.\:\geqslant\:\mathrm{53} \\ $$
Commented by Tinkutara last updated on 12/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
