
Question Number 193253 by MATHEMATICSAM last updated on 08/Jun/23

$$\boldsymbol{\mathrm{Select}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{correct}}\:\boldsymbol{\mathrm{option}}\:\boldsymbol{\mathrm{with}}\: \\ $$$$\boldsymbol{\mathrm{explaination}}: \\ $$$$\mathrm{If}\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{log}_{\mathrm{3}} {M}\:+\:\mathrm{3log}_{\mathrm{3}} {N}\:=\:\mathrm{1}\:+\:\mathrm{log}_{\mathrm{0}.\mathrm{008}} \mathrm{5}\:\mathrm{then} \\ $$$$\mathrm{a}.\:{M}^{\mathrm{9}} \:=\:\frac{\mathrm{9}}{{N}} \\ $$$$\mathrm{b}.\:{N}^{\mathrm{9}} \:=\:\frac{\mathrm{9}}{{M}} \\ $$$$\mathrm{c}.\:{M}^{\mathrm{3}} \:=\:\frac{\mathrm{3}}{{N}} \\ $$$$\mathrm{d}.\:{N}^{\mathrm{3}} \:=\:\frac{\mathrm{3}}{{M}}\: \\ $$
Answered by deleteduser1 last updated on 08/Jun/23
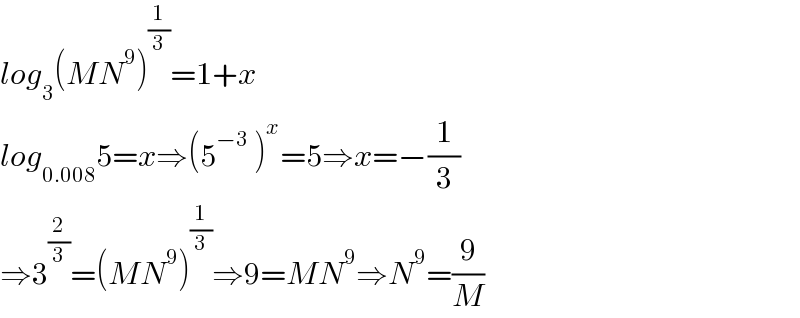
$${log}_{\mathrm{3}} \left({MN}^{\mathrm{9}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{1}+{x} \\ $$$${log}_{\mathrm{0}.\mathrm{008}} \mathrm{5}={x}\Rightarrow\left(\mathrm{5}^{−\mathrm{3}} \:\right)^{{x}} =\mathrm{5}\Rightarrow{x}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{3}^{\frac{\mathrm{2}}{\mathrm{3}}} =\left({MN}^{\mathrm{9}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \Rightarrow\mathrm{9}={MN}^{\mathrm{9}} \Rightarrow{N}^{\mathrm{9}} =\frac{\mathrm{9}}{{M}} \\ $$
