
Question Number 192204 by naka3546 last updated on 11/May/23
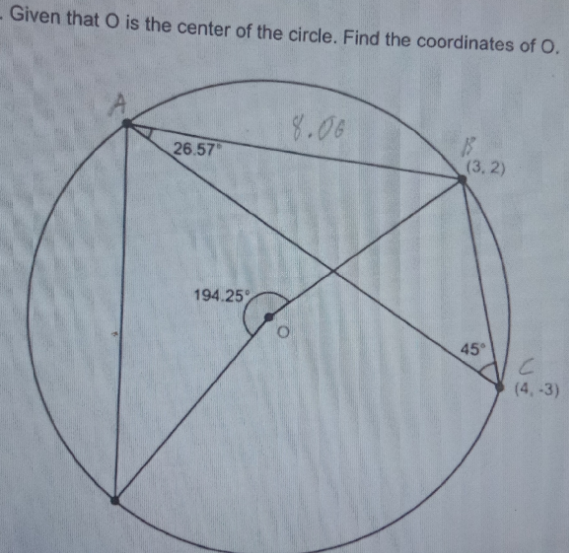
Answered by a.lgnaoui last updated on 11/May/23

$$\mathrm{soit}:\:\:\boldsymbol{\mathrm{C}}\left(\boldsymbol{\mathrm{O}},\boldsymbol{\mathrm{R}}\right)\:\:\:\boldsymbol{\mathrm{C}}\mathrm{entre}\boldsymbol{\mathrm{O}}\left(\boldsymbol{\mathrm{a}},\mathrm{b}\right) \\ $$$$\boldsymbol{\mathrm{equatin}}\:\boldsymbol{\mathrm{cercle}}\:\left(\boldsymbol{\mathrm{origine}}\:\boldsymbol{\mathrm{O}}\right) \\ $$$$\:\:\:\:\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{a}}\right)^{\mathrm{2}} +\left(\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{b}}\right)^{\mathrm{2}} =\boldsymbol{\mathrm{R}}^{\mathrm{2}} \:\:\:\:\:\:\:\:\left(\boldsymbol{\mathrm{E}}\right) \\ $$$$\boldsymbol{\mathrm{Points}}:\:\:\boldsymbol{\mathrm{C}}\:\boldsymbol{\mathrm{et}}\:\:\boldsymbol{\mathrm{B}}\:\:\boldsymbol{\mathrm{verrifient}} \\ $$$$\begin{cases}{\left(\mathrm{4}−\boldsymbol{\mathrm{a}}\right)^{\mathrm{2}} +\left(−\mathrm{3}−\boldsymbol{\mathrm{b}}\right)^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} \:\:\:\:\:\left(\mathrm{1}\right)}\\{\left(\mathrm{3}−\mathrm{a}\right)^{\mathrm{2}} \:\:+\:\:\:\left(\mathrm{2}−\mathrm{b}\right)^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} \:\:\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\:\:\: \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\Rightarrow\:\:\:\boldsymbol{\mathrm{a}}−\mathrm{5}\boldsymbol{\mathrm{b}}=\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$\mathrm{distance}\:\mathrm{BC}=\sqrt{\left(\mathrm{4}−\mathrm{3}\right)^{\mathrm{2}} +\left(−\mathrm{5}\right)^{\mathrm{2}} \:}\:=\sqrt{\mathrm{26}} \\ $$$$\boldsymbol{\mathrm{le}}\:\boldsymbol{\mathrm{point}}\:\boldsymbol{\mathrm{C}}\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)\:\:\mathrm{a}\:\mathrm{pour}\:\mathrm{coordonnes} \\ $$$$\bigtriangleup\boldsymbol{\mathrm{ABC}}\:\:\:\boldsymbol{\mathrm{AC}}=\sqrt{\left(\mathrm{4}−\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} +\left(\mathrm{3}+\boldsymbol{\mathrm{y}}\right)^{\mathrm{2}} } \\ $$$$°\:\:\:\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{A}}} >\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{C}}} \:\:\:\:\:\:\:\:\mathrm{x}_{\mathrm{A}} <\mathrm{x}_{\mathrm{c}} \\ $$$$\boldsymbol{\mathrm{AC}}^{\mathrm{2}} =\mathrm{26}+\left(\mathrm{8},\mathrm{06}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{8},\mathrm{06}×\sqrt{\mathrm{26}}\:\right)\mathrm{cos}\:\left(\mathrm{118}\right) \\ $$$$=\mathrm{116},\mathrm{949583656}\:\:\:\:\:\:\mathrm{AC}=\mathrm{10},\mathrm{81432}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{cases}{}\\{}\end{cases} \\ $$$$\left(\mathrm{E}\right)\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{2}\left(\boldsymbol{\mathrm{ax}}+\boldsymbol{\mathrm{by}}\right)=\boldsymbol{\mathrm{R}}^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{a}}=\mathrm{6}+\mathrm{5}\boldsymbol{\mathrm{b}} \\ $$$$\boldsymbol{\mathrm{d}}\:\mathrm{a}\boldsymbol{\mathrm{pres}}\:\boldsymbol{\mathrm{propriete}}\:\boldsymbol{\mathrm{du}}\:\boldsymbol{\mathrm{centre}}\:\boldsymbol{\mathrm{cercle}}\:\boldsymbol{\mathrm{O}} \\ $$$$\mathrm{2}\measuredangle\boldsymbol{\mathrm{BCA}}=\measuredangle\boldsymbol{\mathrm{BOA}}=\mathrm{90} \\ $$$$\Rightarrow\bigtriangleup\boldsymbol{\mathrm{OAB}}\:\:\:\boldsymbol{\mathrm{triangle}}\:\boldsymbol{\mathrm{rectangle}}\: \\ $$$$\boldsymbol{\mathrm{OA}}^{\mathrm{2}} +\boldsymbol{\mathrm{OB}}^{\mathrm{2}} =\boldsymbol{\mathrm{R}}^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{OA}}=\boldsymbol{\mathrm{OB}}=\boldsymbol{\mathrm{R}}\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\boldsymbol{\mathrm{R}}=\frac{\boldsymbol{\mathrm{AB}}\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{5},\mathrm{699} \\ $$$$\:\mathrm{d}\:\mathrm{apres}\left(\:\boldsymbol{\mathrm{E}}\right)\:\left(\:\:\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{a}}\right)^{\mathrm{2}} +\left(\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{b}}\right)^{\mathrm{2}} =\mathrm{32},\mathrm{478} \\ $$$$\boldsymbol{\mathrm{aplique}}\:\boldsymbol{\mathrm{au}}\:\boldsymbol{\mathrm{pont}}\:\left(\boldsymbol{\mathrm{BC}}\right) \\ $$$$\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\begin{cases}{\left(\mathrm{4}−\mathrm{a}\right)^{\mathrm{2}} +\left(−\mathrm{3}+\frac{\mathrm{6}−\mathrm{a}}{\mathrm{5}}\right)^{\mathrm{2}} =\mathrm{32},\mathrm{478}\:\:\left(\mathrm{1}\right)}\\{\left(\mathrm{3}−\mathrm{a}\right)^{\mathrm{2}} +\left(\mathrm{2}+\frac{\mathrm{6}−\mathrm{a}}{\mathrm{5}}\right)^{\mathrm{2}} \:\:\:\:=\mathrm{32},\mathrm{478}\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\mathrm{choisissons}\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{8a}−\mathrm{6}\left(\frac{\mathrm{6}−\mathrm{a}}{\mathrm{5}}\right)+\mathrm{25}+\left(\frac{\mathrm{6}−\mathrm{a}}{\mathrm{5}}\right)^{\mathrm{2}} =\mathrm{32},\mathrm{478} \\ $$$$\mathrm{25}\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{200}\boldsymbol{\mathrm{a}}−\mathrm{30}\left(\mathrm{6}−\boldsymbol{\mathrm{a}}\right)+\mathrm{25}^{\mathrm{2}} +\left(\mathrm{6}−\boldsymbol{\mathrm{a}}\right)^{\mathrm{2}} =\mathrm{32},\mathrm{478}×\mathrm{25} \\ $$$$\mathrm{26}\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{182}\boldsymbol{\mathrm{a}}+\mathrm{481}=\mathrm{32},\mathrm{478}×\mathrm{25}^{\mathrm{2}} \\ $$$$\:\:\:\boldsymbol{\mathrm{a}}^{\mathrm{2}} −\mathrm{7}\boldsymbol{\mathrm{a}}−\mathrm{781},\mathrm{25}=\mathrm{0} \\ $$$$\bigtriangleup=\mathrm{49}+\mathrm{3125}=\mathrm{3174}=\mathrm{23}\sqrt{\mathrm{6}} \\ $$$$\:\:\boldsymbol{\mathrm{a}}=\frac{\mathrm{7}\pm\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}}\Rightarrow\begin{cases}{\mathrm{a}=\frac{\mathrm{7}+\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}}\:\:\:\:\:\:\:\left(\mathrm{1}\right)}\\{\mathrm{a}=\frac{\mathrm{7}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}}\:\:\:\:\:\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\:\: \\ $$$$\:\:\:\:\boldsymbol{\mathrm{b}}=\frac{\boldsymbol{\mathrm{a}}−\mathrm{6}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{b}}=\:\frac{\mathrm{23}\sqrt{\mathrm{6}}\:+\mathrm{1}}{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{b}}=\frac{\mathrm{6}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{10}} \\ $$$$\boldsymbol{\mathrm{donc}}\:\boldsymbol{\mathrm{les}}\:\boldsymbol{\mathrm{coordonnes}}\:\boldsymbol{\mathrm{possibles}}\:\boldsymbol{\mathrm{d}}\mathrm{u}\:\boldsymbol{\mathrm{centr}}\:\boldsymbol{\mathrm{O}}\:\boldsymbol{\mathrm{sont}}: \\ $$$$\:\:\left(\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}\right)=\left\{\left(\frac{\mathrm{7}+\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}}\:,\frac{\mathrm{23}\sqrt{\mathrm{6}}\:+\mathrm{1}}{\mathrm{10}}\right)\:\:\:\:,\:\:\left(\frac{\mathrm{7}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}},\frac{\mathrm{6}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{10}}\right)\right\} \\ $$$$\mathrm{equation}\:\:\mathrm{2}\Rightarrow \\ $$$$\mathrm{13}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\left(\mathrm{6}\boldsymbol{\mathrm{a}}+\mathrm{4}\boldsymbol{\mathrm{b}}\right)=\boldsymbol{\mathrm{R}}^{\mathrm{2}} \\ $$$$\left(\mathrm{y}−\mathrm{b}\right)^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} −\left(\mathrm{x}−\mathrm{a}\right)^{\mathrm{2}} \\ $$$$\mathrm{y}=\sqrt{\boldsymbol{\mathrm{R}}^{\mathrm{2}} −\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{a}}\right)^{\mathrm{2}} }\:+\boldsymbol{\mathrm{b}}\:\:\: \\ $$$$\boldsymbol{\mathrm{R}}^{\mathrm{2}} −\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{a}}\right)^{\mathrm{2}} >\mathrm{0}\:\:\:\:\:\boldsymbol{\mathrm{R}}>\mid\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{a}}\mid \\ $$$$\begin{cases}{\mathrm{x}\boldsymbol{\mathrm{c}}=\mathrm{4}>\mathrm{0}}\\{\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{c}}} <\mathrm{0}}\end{cases}\:\Rightarrow\:\mathrm{4}−\frac{\mathrm{7}+\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}}=\frac{\mathrm{8}−\mathrm{7}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}}<\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{y}<\mathrm{0} \\ $$$$\mathrm{donc}\:\:\:\:\mathrm{la}\:\mathrm{valeur}\:\mathrm{de}\:\:\mathrm{a}\:\mathrm{acceptee}\:\mathrm{est}\: \\ $$$$\mathrm{a}=\frac{\mathrm{7}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}}\:\:\:\:\:\mathrm{soit}\:\:\mathrm{b}=\frac{\mathrm{6}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{10}} \\ $$$$ \\ $$$$\:\:\:\boldsymbol{\mathrm{donc}}:\:\:\:\:\boldsymbol{\mathrm{O}}\left(\frac{\mathrm{7}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{2}}\:,\frac{\mathrm{6}−\mathrm{23}\sqrt{\mathrm{6}}}{\mathrm{10}}\right)\:\:\: \\ $$$$ \\ $$
Commented by naka3546 last updated on 12/May/23

$$\mathrm{Thank}\:\:\mathrm{you} \\ $$
