
Question Number 192126 by universe last updated on 08/May/23
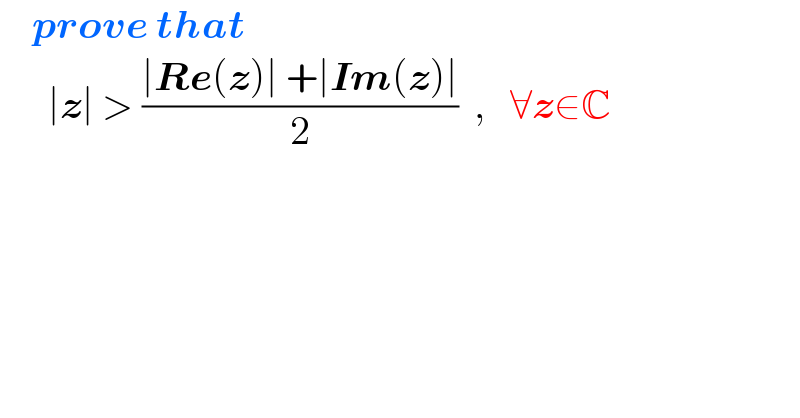
$$\:\:\:\:\boldsymbol{{prove}}\:\boldsymbol{{that}} \\ $$ $$\:\:\:\:\:\:\mid\boldsymbol{{z}}\mid\:>\:\frac{\mid\boldsymbol{{Re}}\left(\boldsymbol{{z}}\right)\mid\:+\mid\boldsymbol{{Im}}\left(\boldsymbol{{z}}\right)\mid}{\mathrm{2}}\:\:,\:\:\:\forall\boldsymbol{{z}}\in\mathbb{C} \\ $$
Commented byYork12 last updated on 09/May/23
$${sir}\:{how}\:{can}\:{I}\:{reach}\:{you}\:{out}\:,\:{I}\:{need}\:{to}\:{ask}\:{several}\:{questions} \\ $$
Answered by AST last updated on 08/May/23
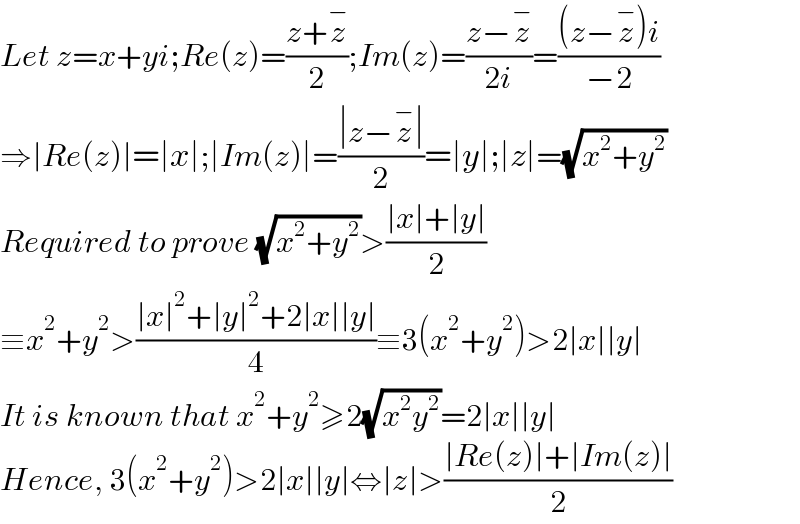
$${Let}\:{z}={x}+{yi};{Re}\left({z}\right)=\frac{{z}+\overset{−} {{z}}}{\mathrm{2}};{Im}\left({z}\right)=\frac{{z}−\overset{−} {{z}}}{\mathrm{2}{i}}=\frac{\left({z}−\overset{−} {{z}}\right){i}}{−\mathrm{2}} \\ $$ $$\Rightarrow\mid{Re}\left({z}\right)\mid=\mid{x}\mid;\mid{Im}\left({z}\right)\mid=\frac{\mid{z}−\overset{−} {{z}}\mid}{\mathrm{2}}=\mid{y}\mid;\mid{z}\mid=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$ $${Required}\:{to}\:{prove}\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }>\frac{\mid{x}\mid+\mid{y}\mid}{\mathrm{2}} \\ $$ $$\equiv{x}^{\mathrm{2}} +{y}^{\mathrm{2}} >\frac{\mid{x}\mid^{\mathrm{2}} +\mid{y}\mid^{\mathrm{2}} +\mathrm{2}\mid{x}\mid\mid{y}\mid}{\mathrm{4}}\equiv\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)>\mathrm{2}\mid{x}\mid\mid{y}\mid \\ $$ $${It}\:{is}\:{known}\:{that}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \geqslant\mathrm{2}\sqrt{{x}^{\mathrm{2}} {y}^{\mathrm{2}} }=\mathrm{2}\mid{x}\mid\mid{y}\mid \\ $$ $${Hence},\:\mathrm{3}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)>\mathrm{2}\mid{x}\mid\mid{y}\mid\Leftrightarrow\mid{z}\mid>\frac{\mid{Re}\left({z}\right)\mid+\mid{Im}\left({z}\right)\mid}{\mathrm{2}} \\ $$
Answered by mehdee42 last updated on 08/May/23
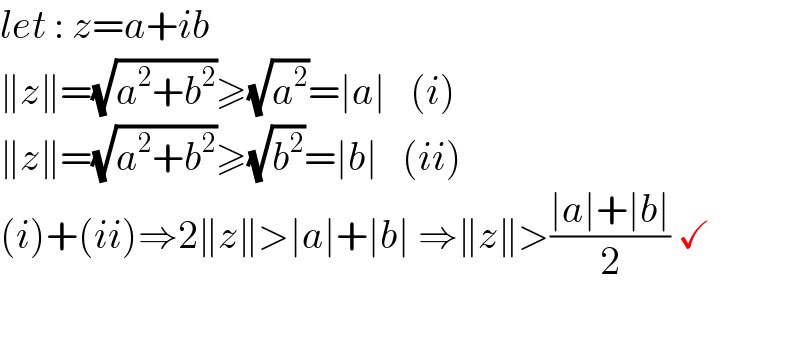
$${let}\::\:{z}={a}+{ib} \\ $$ $$\parallel{z}\parallel=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\geqslant\sqrt{{a}^{\mathrm{2}} }=\mid{a}\mid\:\:\:\left({i}\right) \\ $$ $$\parallel{z}\parallel=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\geqslant\sqrt{{b}^{\mathrm{2}} }=\mid{b}\mid\:\:\:\left({ii}\right) \\ $$ $$\left({i}\right)+\left({ii}\right)\Rightarrow\mathrm{2}\parallel{z}\parallel>\mid{a}\mid+\mid{b}\mid\:\Rightarrow\parallel{z}\parallel>\frac{\mid{a}\mid+\mid{b}\mid}{\mathrm{2}}\:\checkmark \\ $$ $$ \\ $$
