
Previous in Differential Equation Next in Differential Equation
Question Number 19199 by priyankavarma094@gmail.com last updated on 06/Aug/17
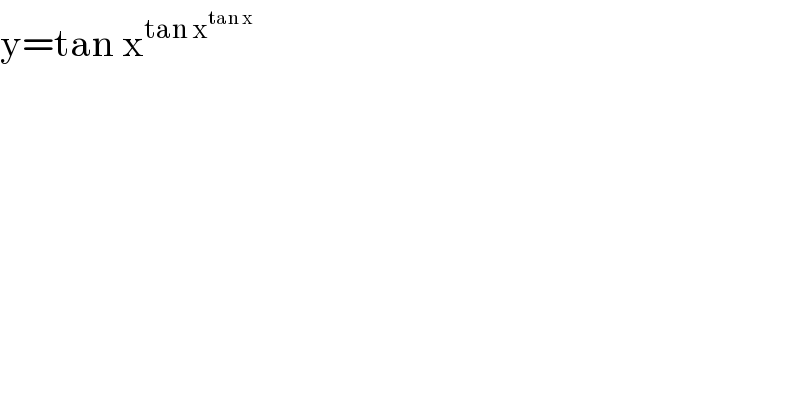
$$\mathrm{y}=\mathrm{tan}\:\mathrm{x}^{\mathrm{tan}\:\mathrm{x}^{\mathrm{tan}\:\mathrm{x}} } \\ $$
Answered by NEC last updated on 06/Aug/17
![let u=tan x y=u^u^u ln y=u^u ln u (1/y)dy/dx=u^u ((1/u))+(u^u +ln u)ln u (dy/dx)=y[(u^u .(1/u) + (u^u +ln u)ln u)] (dy/dx)=tanx^(tanx^(tanx ) ) {(tanx^(tan x−1) +(tanx^(tanx ) +ln tan x)ln tan x)}](Q19202.png)
$${let}\:{u}=\mathrm{tan}\:{x} \\ $$$$ \\ $$$${y}={u}^{{u}^{{u}} } \\ $$$$\mathrm{ln}\:{y}={u}^{{u}} \mathrm{ln}\:{u} \\ $$$$\frac{\mathrm{1}}{{y}}{dy}/{dx}={u}^{{u}} \left(\frac{\mathrm{1}}{{u}}\right)+\left({u}^{{u}} +\mathrm{ln}\:{u}\right)\mathrm{ln}\:{u} \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}={y}\left[\left({u}^{{u}} .\frac{\mathrm{1}}{{u}}\:+\:\left({u}^{{u}} +\mathrm{ln}\:{u}\right)\mathrm{ln}\:{u}\right)\right] \\ $$$$\frac{{dy}}{{dx}}=\mathrm{tan}{x}\:^{\mathrm{tan}{x}\:^{\mathrm{tan}{x}\:} } \left\{\left(\mathrm{tan}{x}\:^{\mathrm{tan}\:{x}−\mathrm{1}} \:+\left(\mathrm{tan}{x}\:^{\mathrm{tan}{x}\:} +\mathrm{ln}\:\mathrm{tan}\:{x}\right)\mathrm{ln}\:\mathrm{tan}\:{x}\right)\right\} \\ $$
Commented by NEC last updated on 06/Aug/17
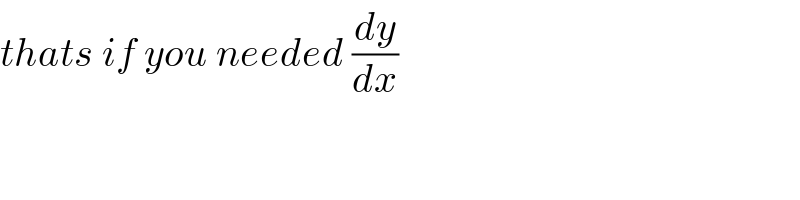
$${thats}\:{if}\:{you}\:{needed}\:\frac{{dy}}{{dx}} \\ $$
