
Question Number 76615 by mhmd last updated on 28/Dec/19

$$\int{sec}^{\mathrm{3}} {x}\:{dx} \\ $$
Answered by $@ty@m123 last updated on 28/Dec/19
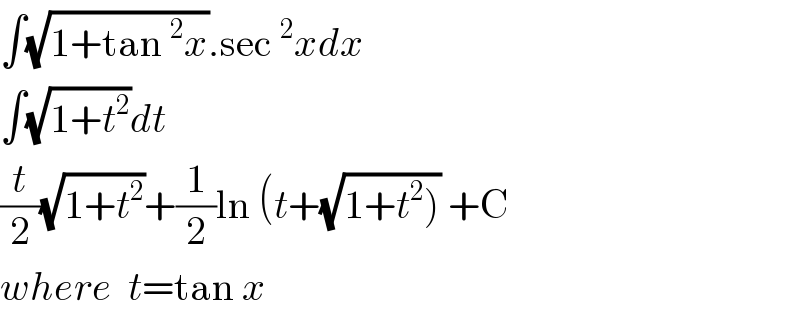
$$\int\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}}.\mathrm{sec}\:^{\mathrm{2}} {xdx} \\ $$$$\int\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\frac{{t}}{\mathrm{2}}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}+\sqrt{\left.\mathrm{1}+{t}^{\mathrm{2}} \right)}\:+\mathrm{C}\right. \\ $$$${where}\:\:{t}=\mathrm{tan}\:{x} \\ $$
Answered by john santu last updated on 29/Dec/19
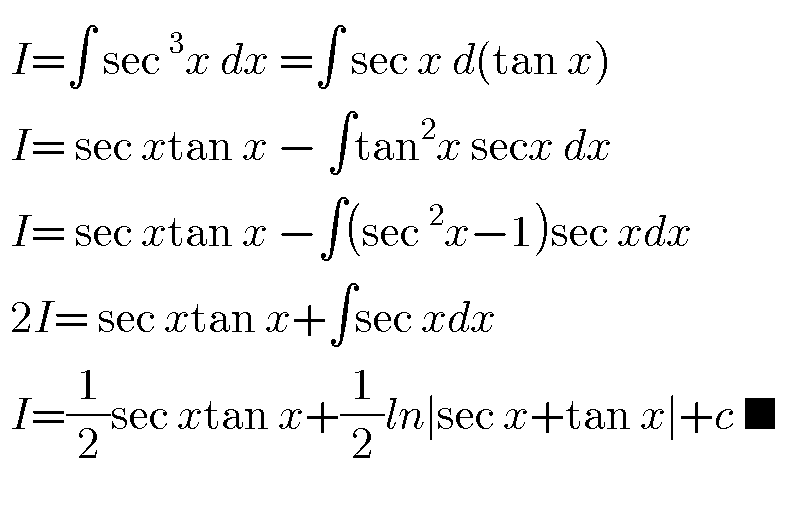
Commented by mhmd last updated on 29/Dec/19

$${thank}\:{you}\:{sir} \\ $$
Commented by john santu last updated on 29/Dec/19

$${your}\:{welcome}\:{sir} \\ $$
