
Question Number 190115 by HeferH last updated on 27/Mar/23
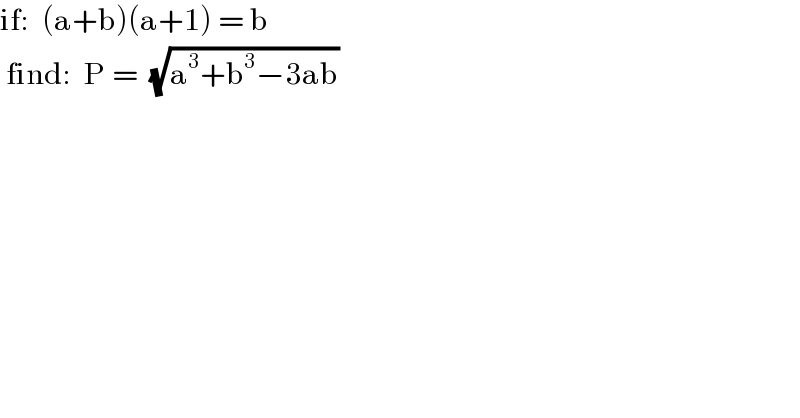
$$\mathrm{if}:\:\:\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}+\mathrm{1}\right)\:=\:\mathrm{b} \\ $$$$\:\mathrm{find}:\:\:\mathrm{P}\:=\:\:\sqrt{\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} −\mathrm{3ab}} \\ $$
Answered by som(math1967) last updated on 27/Mar/23
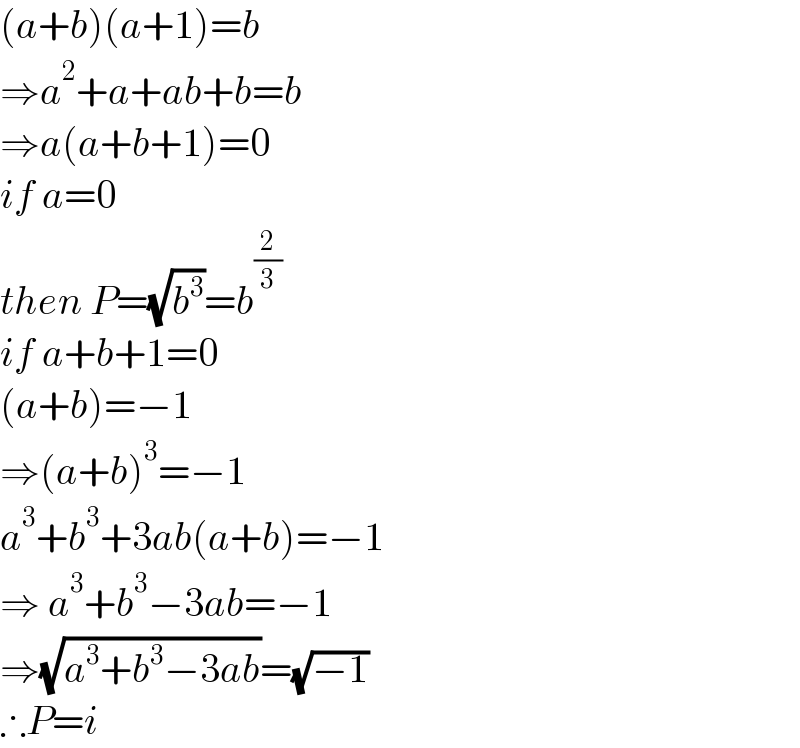
$$\left({a}+{b}\right)\left({a}+\mathrm{1}\right)={b} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{a}+{ab}+{b}={b} \\ $$$$\Rightarrow{a}\left({a}+{b}+\mathrm{1}\right)=\mathrm{0} \\ $$$${if}\:{a}=\mathrm{0} \\ $$$${then}\:{P}=\sqrt{{b}^{\mathrm{3}} }={b}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$${if}\:{a}+{b}+\mathrm{1}=\mathrm{0} \\ $$$$\left({a}+{b}\right)=−\mathrm{1} \\ $$$$\Rightarrow\left({a}+{b}\right)^{\mathrm{3}} =−\mathrm{1} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right)=−\mathrm{1} \\ $$$$\Rightarrow\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} −\mathrm{3}{ab}=−\mathrm{1} \\ $$$$\Rightarrow\sqrt{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} −\mathrm{3}{ab}}=\sqrt{−\mathrm{1}} \\ $$$$\therefore{P}={i} \\ $$
Commented by HeferH last updated on 27/Mar/23

$$\mathrm{Thanks}! \\ $$
