Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 190091 by Shrinava last updated on 27/Mar/23

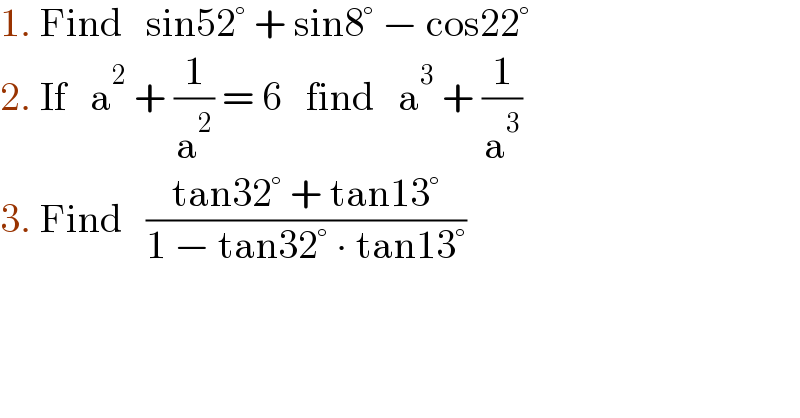
1. Find sin52° + sin8° − cos22° 2. If a^2 + (1/a^2 ) = 6 find a^3 + (1/a^3 ) 3. Find ((tan32° + tan13°)/(1 − tan32° ∙ tan13°))

$$\mathrm{1}.\:\mathrm{Find}\:\:\:\mathrm{sin52}°\:+\:\mathrm{sin8}°\:−\:\mathrm{cos22}° \\ $$$$\mathrm{2}.\:\mathrm{If}\:\:\:\mathrm{a}^{\mathrm{2}} \:+\:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }\:=\:\mathrm{6}\:\:\:\mathrm{find}\:\:\:\mathrm{a}^{\mathrm{3}} \:+\:\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} } \\ $$$$\mathrm{3}.\:\mathrm{Find}\:\:\:\frac{\mathrm{tan32}°\:+\:\mathrm{tan13}°}{\mathrm{1}\:−\:\mathrm{tan32}°\:\centerdot\:\mathrm{tan13}°} \\ $$

Answered by BaliramKumar last updated on 27/Mar/23

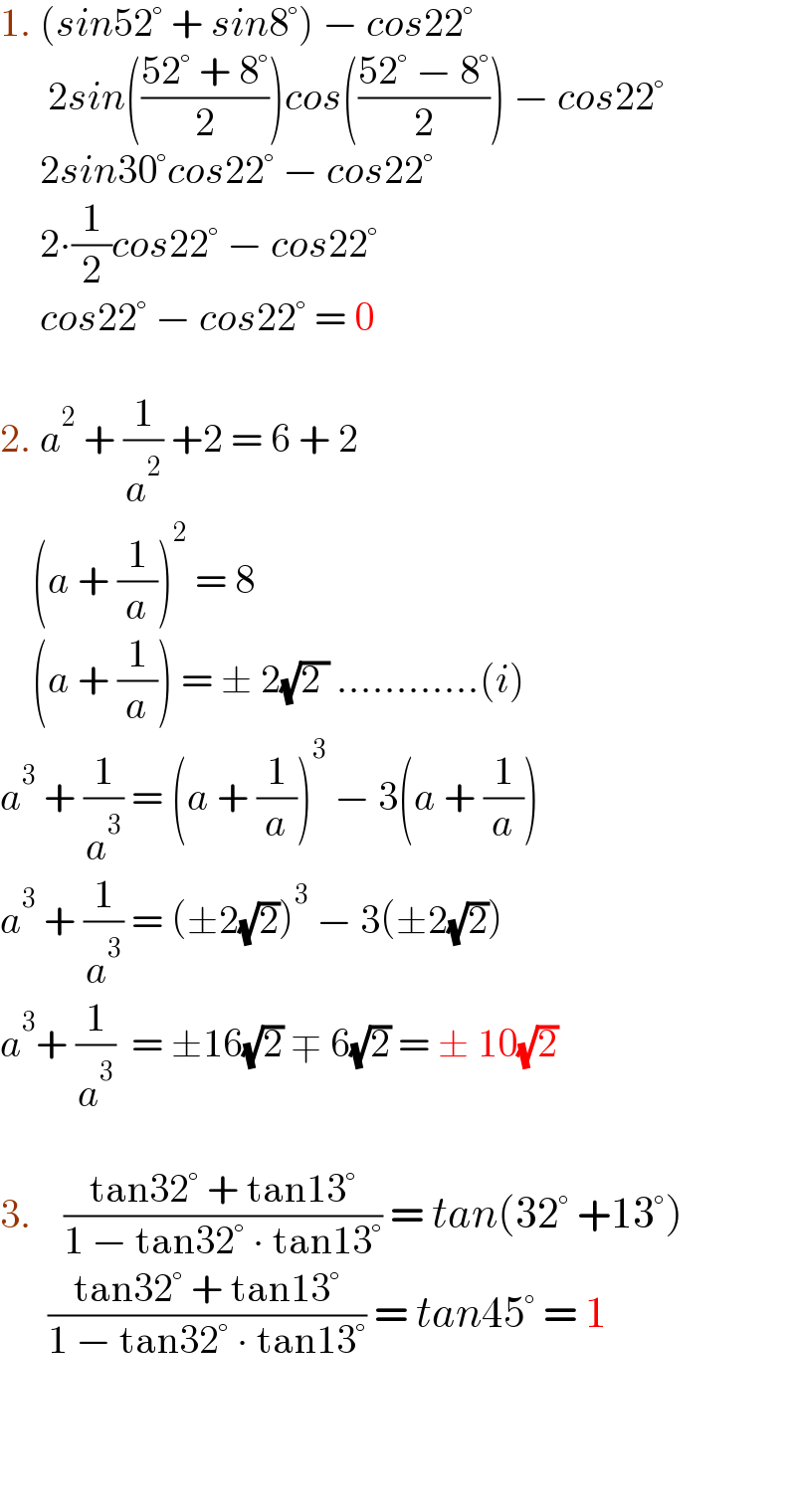
1. (sin52° + sin8°) − cos22° 2sin(((52° + 8°)/2))cos(((52° − 8°)/2)) − cos22° 2sin30°cos22° − cos22° 2∙(1/2)cos22° − cos22° cos22° − cos22° = 0 2. a^2 + (1/a^2 ) +2 = 6 + 2 (a + (1/a))^2 = 8 (a + (1/a)) = ± 2(√(2 )) ............(i) a^3 + (1/a^3 ) = (a + (1/a))^3 − 3(a + (1/a)) a^3 + (1/a^3 ) = (±2(√2))^3 − 3(±2(√2)) a^3 + (1/a^3 ) = ±16(√2) ∓ 6(√2) = ± 10(√2) 3. ((tan32° + tan13°)/(1 − tan32° ∙ tan13°)) = tan(32° +13°) ((tan32° + tan13°)/(1 − tan32° ∙ tan13°)) = tan45° = 1

$$\mathrm{1}.\:\left({sin}\mathrm{52}°\:+\:{sin}\mathrm{8}°\right)\:−\:{cos}\mathrm{22}° \\ $$$$\:\:\:\:\:\:\mathrm{2}{sin}\left(\frac{\mathrm{52}°\:+\:\mathrm{8}°}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{52}°\:−\:\mathrm{8}°}{\mathrm{2}}\right)\:−\:{cos}\mathrm{22}° \\ $$$$\:\:\:\:\:\mathrm{2}{sin}\mathrm{30}°{cos}\mathrm{22}°\:−\:{cos}\mathrm{22}° \\ $$$$\:\:\:\:\:\mathrm{2}\centerdot\frac{\mathrm{1}}{\mathrm{2}}{cos}\mathrm{22}°\:−\:{cos}\mathrm{22}° \\ $$$$\:\:\:\:\:{cos}\mathrm{22}°\:−\:{cos}\mathrm{22}°\:=\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{2}.\:{a}^{\mathrm{2}} \:+\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:+\mathrm{2}\:=\:\mathrm{6}\:+\:\mathrm{2} \\ $$$$\:\:\:\:\left({a}\:+\:\frac{\mathrm{1}}{{a}}\right)^{\mathrm{2}} \:=\:\mathrm{8} \\ $$$$\:\:\:\:\left({a}\:+\:\frac{\mathrm{1}}{{a}}\right)\:=\:\pm\:\mathrm{2}\sqrt{\mathrm{2}\:}\:............\left({i}\right) \\ $$$${a}^{\mathrm{3}} \:+\:\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\:=\:\left({a}\:+\:\frac{\mathrm{1}}{{a}}\right)^{\mathrm{3}} \:−\:\mathrm{3}\left({a}\:+\:\frac{\mathrm{1}}{{a}}\right) \\ $$$${a}^{\mathrm{3}} \:+\:\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\:=\:\left(\pm\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{3}} \:−\:\mathrm{3}\left(\pm\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$$${a}^{\mathrm{3}} +\:\frac{\mathrm{1}}{{a}^{\mathrm{3}} }\:\:=\:\pm\mathrm{16}\sqrt{\mathrm{2}}\:\mp\:\mathrm{6}\sqrt{\mathrm{2}}\:=\:\pm\:\mathrm{10}\sqrt{\mathrm{2}} \\ $$$$\: \\ $$$$\mathrm{3}.\:\:\:\:\frac{\mathrm{tan32}°\:+\:\mathrm{tan13}°}{\mathrm{1}\:−\:\mathrm{tan32}°\:\centerdot\:\mathrm{tan13}°}\:=\:{tan}\left(\mathrm{32}°\:+\mathrm{13}°\right) \\ $$$$\:\:\:\:\:\:\frac{\mathrm{tan32}°\:+\:\mathrm{tan13}°}{\mathrm{1}\:−\:\mathrm{tan32}°\:\centerdot\:\mathrm{tan13}°}\:=\:{tan}\mathrm{45}°\:=\:\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Shrinava last updated on 01/Apr/23

thank you professor cool

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{professor}\:\mathrm{cool} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com