
Question Number 18940 by Tinkutara last updated on 01/Aug/17

$$\mathrm{A}\:\mathrm{light}\:\mathrm{rope}\:\mathrm{is}\:\mathrm{passed}\:\mathrm{over}\:\mathrm{a}\:\mathrm{pulley}\:\mathrm{such} \\ $$$$\mathrm{that}\:\mathrm{at}\:\mathrm{its}\:\mathrm{one}\:\mathrm{end}\:\mathrm{a}\:\mathrm{block}\:\mathrm{is}\:\mathrm{attached}, \\ $$$$\mathrm{and}\:\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{end}\:\mathrm{a}\:\mathrm{boy}\:\mathrm{is}\:\mathrm{climbing} \\ $$$$\mathrm{up}\:\mathrm{with}\:\mathrm{acceleration}\:\frac{{g}}{\mathrm{2}}\:\mathrm{relative}\:\mathrm{to}\:\mathrm{rope}. \\ $$$$\mathrm{Mass}\:\mathrm{of}\:\mathrm{the}\:\mathrm{block}\:\mathrm{is}\:\mathrm{30}\:\mathrm{kg}\:\mathrm{and}\:\mathrm{that}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{boy}\:\mathrm{is}\:\mathrm{40}\:\mathrm{kg}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{tension}\:\mathrm{and} \\ $$$$\mathrm{acceleration}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rope}. \\ $$
Commented by ajfour last updated on 01/Aug/17
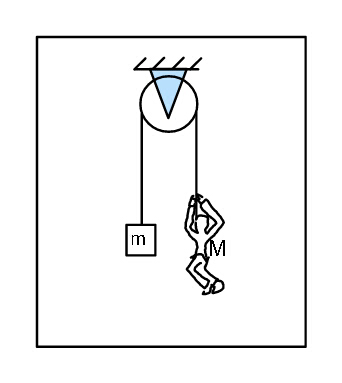
Commented by ajfour last updated on 01/Aug/17
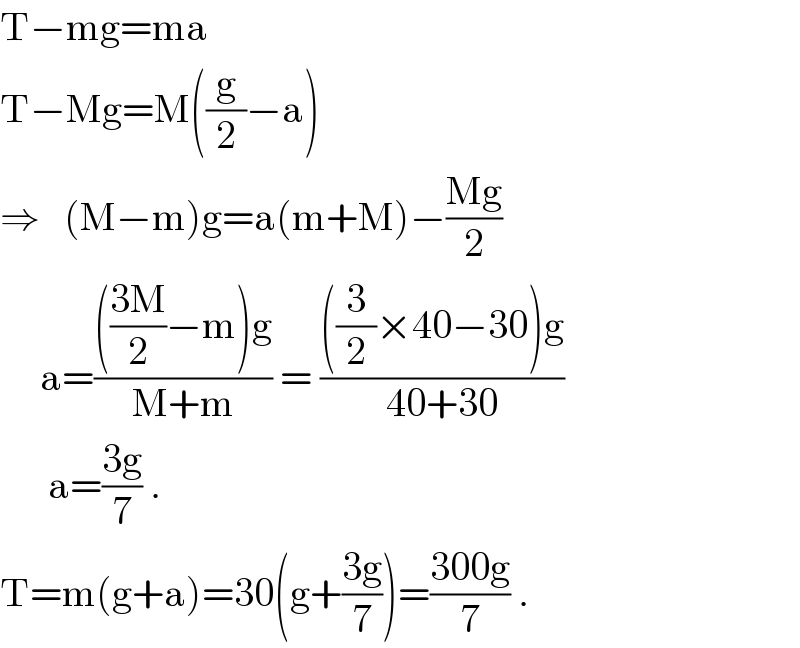
$$\mathrm{T}−\mathrm{mg}=\mathrm{ma} \\ $$$$\mathrm{T}−\mathrm{Mg}=\mathrm{M}\left(\frac{\mathrm{g}}{\mathrm{2}}−\mathrm{a}\right) \\ $$$$\Rightarrow\:\:\:\left(\mathrm{M}−\mathrm{m}\right)\mathrm{g}=\mathrm{a}\left(\mathrm{m}+\mathrm{M}\right)−\frac{\mathrm{Mg}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{a}=\frac{\left(\frac{\mathrm{3M}}{\mathrm{2}}−\mathrm{m}\right)\mathrm{g}}{\mathrm{M}+\mathrm{m}}\:=\:\frac{\left(\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{40}−\mathrm{30}\right)\mathrm{g}}{\mathrm{40}+\mathrm{30}} \\ $$$$\:\:\:\:\:\:\mathrm{a}=\frac{\mathrm{3g}}{\mathrm{7}}\:.\: \\ $$$$\mathrm{T}=\mathrm{m}\left(\mathrm{g}+\mathrm{a}\right)=\mathrm{30}\left(\mathrm{g}+\frac{\mathrm{3g}}{\mathrm{7}}\right)=\frac{\mathrm{300g}}{\mathrm{7}}\:. \\ $$
Commented by Tinkutara last updated on 01/Aug/17

$$\mathrm{Wonderful}\:\mathrm{Sir}! \\ $$
