
Question Number 189325 by mnjuly1970 last updated on 14/Mar/23
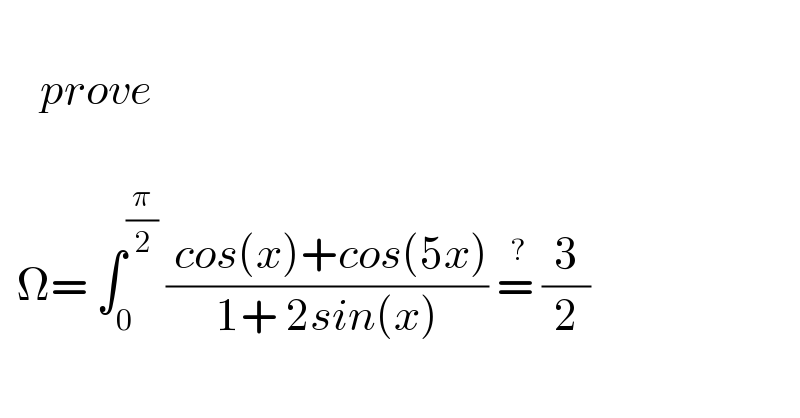
$$ \\ $$$$\:\:\:\:\:{prove} \\ $$$$ \\ $$$$\:\:\Omega=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\:{cos}\left({x}\right)+{cos}\left(\mathrm{5}{x}\right)}{\mathrm{1}+\:\mathrm{2}{sin}\left({x}\right)}\:\overset{\:?} {=}\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by Frix last updated on 15/Mar/23
![∫_0 ^(π/2) ((cos 5x +cos x)/(1+2sin x))dx=^(t=sin x) =2∫_0 ^1 (4t^3 −2t^2 −2t+1)dt= =2[t^4 −((2t^3 )/3)−t^2 +t]_0 ^1 =(2/3)](Q189341.png)
$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{cos}\:\mathrm{5}{x}\:+\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{2sin}\:{x}}{dx}\overset{{t}=\mathrm{sin}\:{x}} {=} \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{4}{t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right){dt}= \\ $$$$=\mathrm{2}\left[{t}^{\mathrm{4}} −\frac{\mathrm{2}{t}^{\mathrm{3}} }{\mathrm{3}}−{t}^{\mathrm{2}} +{t}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 15/Mar/23
$${thankx}\:{alot}\:{sir}\:{frix} \\ $$
Answered by cortano12 last updated on 15/Mar/23
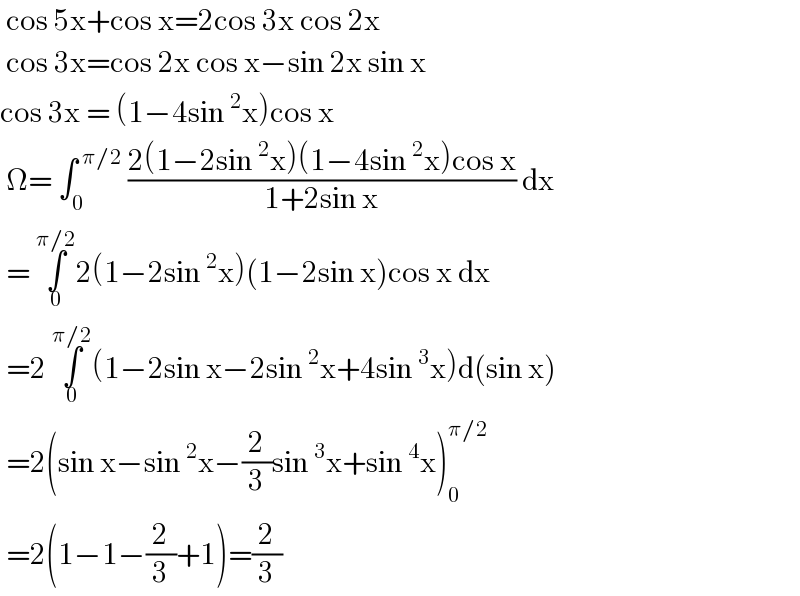
$$\:\mathrm{cos}\:\mathrm{5x}+\mathrm{cos}\:\mathrm{x}=\mathrm{2cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{2x} \\ $$$$\:\mathrm{cos}\:\mathrm{3x}=\mathrm{cos}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{2x}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{cos}\:\mathrm{3x}\:=\:\left(\mathrm{1}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}\right)\mathrm{cos}\:\mathrm{x} \\ $$$$\:\Omega=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}\right)\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{2sin}\:\mathrm{x}}\:\mathrm{dx} \\ $$$$\:=\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{2}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\mathrm{2sin}\:\mathrm{x}\right)\mathrm{cos}\:\mathrm{x}\:\mathrm{dx} \\ $$$$\:=\mathrm{2}\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\left(\mathrm{1}−\mathrm{2sin}\:\mathrm{x}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{4sin}\:^{\mathrm{3}} \mathrm{x}\right)\mathrm{d}\left(\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:=\mathrm{2}\left(\mathrm{sin}\:\mathrm{x}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}\right)_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$\:=\mathrm{2}\left(\mathrm{1}−\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{1}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 15/Mar/23

$$\:\:\:{very}\:{nice}\:{sir}\:{cortano}.. \\ $$
Commented by Spillover last updated on 15/Mar/23
$${nice}\:{solution} \\ $$
