Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 189208 by mathlove last updated on 13/Mar/23

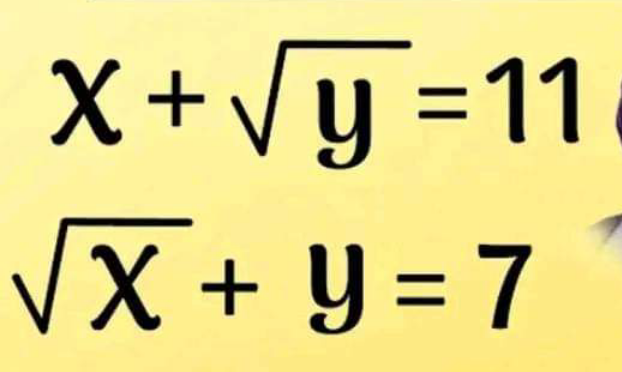
Answered by MJS_new last updated on 13/Mar/23

easy to see 9+2=11 3+4=7 x=9∧y=4

$$\mathrm{easy}\:\mathrm{to}\:\mathrm{see} \\ $$$$\mathrm{9}+\mathrm{2}=\mathrm{11} \\ $$$$\mathrm{3}+\mathrm{4}=\mathrm{7} \\ $$$${x}=\mathrm{9}\wedge{y}=\mathrm{4} \\ $$

Commented by mathlove last updated on 13/Mar/23

solve it???

$${solve}\:{it}??? \\ $$

Commented by MJS_new last updated on 13/Mar/23

another exampke: solve 3+x=5: 3=1+1+1 5=1+1+1+1+1 how many 1s must we add to get from 3 to 5? 1+1+1+1+1=1+1+1+1+1 1+1=2 the answer is 3+2=5 ⇒ x=2 now try to solve your question

$$\mathrm{another}\:\mathrm{exampke}: \\ $$$$\mathrm{solve}\:\mathrm{3}+{x}=\mathrm{5}: \\ $$$$\mathrm{3}=\mathrm{1}+\mathrm{1}+\mathrm{1} \\ $$$$\mathrm{5}=\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1} \\ $$$$\mathrm{how}\:\mathrm{many}\:\mathrm{1s}\:\mathrm{must}\:\mathrm{we}\:\mathrm{add}\:\mathrm{to}\:\mathrm{get}\:\mathrm{from}\:\mathrm{3}\:\mathrm{to}\:\mathrm{5}? \\ $$$$\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}=\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is} \\ $$$$\mathrm{3}+\mathrm{2}=\mathrm{5} \\ $$$$\Rightarrow\:{x}=\mathrm{2} \\ $$$$\mathrm{now}\:\mathrm{try}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{your}\:\mathrm{question} \\ $$

Answered by manxsol last updated on 13/Mar/23

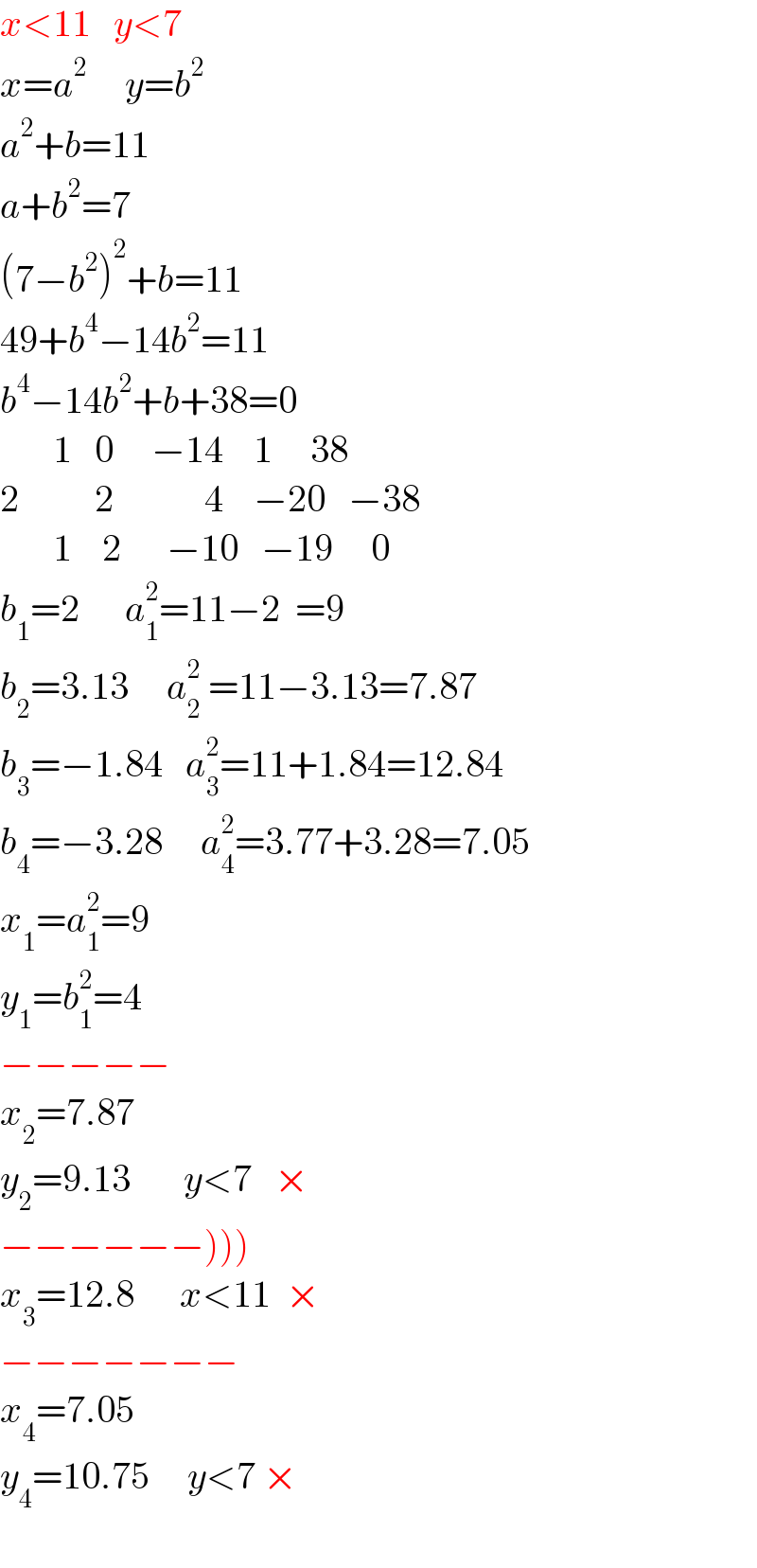
x<11 y<7 x=a^(2 ) y=b^2 a^2 +b=11 a+b^2 =7 (7−b^2 )^2 +b=11 49+b^4 −14b^2 =11 b^4 −14b^2 +b+38=0 1 0 −14 1 38 2 2 4 −20 −38 1 2 −10 −19 0 b_1 =2 a_1 ^2 =11−2 =9 b_2 =3.13 a_2 ^2 =11−3.13=7.87 b_3 =−1.84 a_3 ^2 =11+1.84=12.84 b_4 =−3.28 a_4 ^2 =3.77+3.28=7.05 x_1 =a_1 ^2 =9 y_1 =b_1 ^2 =4 −−−−− x_2 =7.87 y_2 =9.13 y<7 × −−−−−−))) x_3 =12.8 x<11 × −−−−−−− x_4 =7.05 y_4 =10.75 y<7 ×

$${x}<\mathrm{11}\:\:\:{y}<\mathrm{7} \\ $$$${x}={a}^{\mathrm{2}\:\:\:\:} \:\:\:{y}={b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}=\mathrm{11} \\ $$$${a}+{b}^{\mathrm{2}} =\mathrm{7} \\ $$$$\left(\mathrm{7}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} +{b}=\mathrm{11} \\ $$$$\mathrm{49}+{b}^{\mathrm{4}} −\mathrm{14}{b}^{\mathrm{2}} =\mathrm{11} \\ $$$${b}^{\mathrm{4}} −\mathrm{14}{b}^{\mathrm{2}} +{b}+\mathrm{38}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{1}\:\:\:\mathrm{0}\:\:\:\:\:−\mathrm{14}\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{38} \\ $$$$\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:−\mathrm{20}\:\:\:−\mathrm{38} \\ $$$$\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{2}\:\:\:\:\:\:−\mathrm{10}\:\:\:−\mathrm{19}\:\:\:\:\:\mathrm{0} \\ $$$${b}_{\mathrm{1}} =\mathrm{2}\:\:\:\:\:\:{a}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{11}−\mathrm{2}\:\:=\mathrm{9} \\ $$$${b}_{\mathrm{2}} =\mathrm{3}.\mathrm{13}\:\:\:\:\:{a}_{\mathrm{2}} ^{\mathrm{2}} \:=\mathrm{11}−\mathrm{3}.\mathrm{13}=\mathrm{7}.\mathrm{87} \\ $$$${b}_{\mathrm{3}} =−\mathrm{1}.\mathrm{84}\:\:\:{a}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{11}+\mathrm{1}.\mathrm{84}=\mathrm{12}.\mathrm{84} \\ $$$${b}_{\mathrm{4}} =−\mathrm{3}.\mathrm{28}\:\:\:\:\:{a}_{\mathrm{4}} ^{\mathrm{2}} =\mathrm{3}.\mathrm{77}+\mathrm{3}.\mathrm{28}=\mathrm{7}.\mathrm{05} \\ $$$${x}_{\mathrm{1}} ={a}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{9} \\ $$$${y}_{\mathrm{1}} ={b}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{4} \\ $$$$−−−−− \\ $$$${x}_{\mathrm{2}} =\mathrm{7}.\mathrm{87} \\ $$$${y}_{\mathrm{2}} =\mathrm{9}.\mathrm{13}\:\:\:\:\:\:\:{y}<\mathrm{7}\:\:\:× \\ $$$$\left.−\left.−\left.−−−−\right)\right)\right) \\ $$$${x}_{\mathrm{3}} =\mathrm{12}.\mathrm{8}\:\:\:\:\:\:{x}<\mathrm{11}\:\:× \\ $$$$−−−−−−− \\ $$$${x}_{\mathrm{4}} =\mathrm{7}.\mathrm{05} \\ $$$${y}_{\mathrm{4}} =\mathrm{10}.\mathrm{75}\:\:\:\:\:{y}<\mathrm{7}\:× \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com