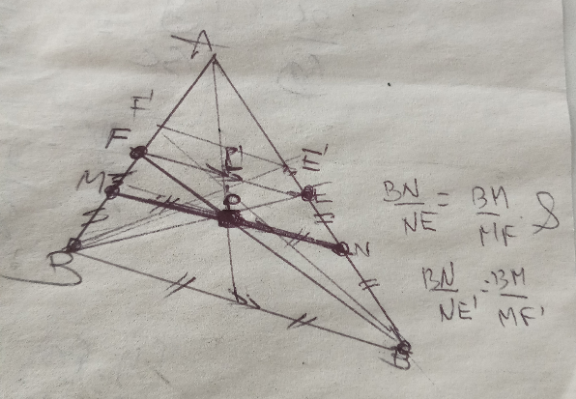
Question Number 189070 by Rupesh123 last updated on 11/Mar/23

Answered by a.lgnaoui last updated on 12/Mar/23
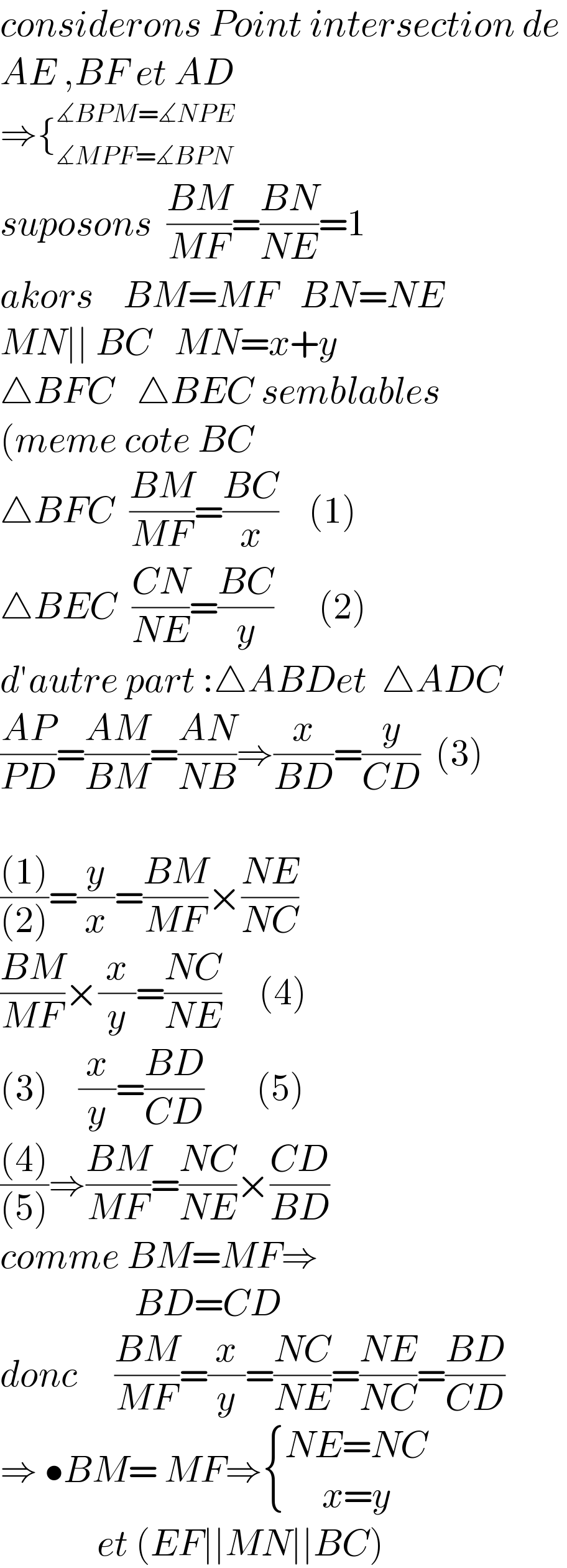
$${considerons}\:{Point}\:{intersection}\:{de}\: \\ $$$${AE}\:,{BF}\:{et}\:{AD}\: \\ $$$$\Rightarrow\left\{_{\measuredangle{MPF}=\measuredangle{BPN}} ^{\measuredangle{BPM}=\measuredangle{NPE}} \right. \\ $$$${suposons}\:\:\frac{{BM}}{{MF}}=\frac{{BN}}{{NE}}=\mathrm{1} \\ $$$${akors}\:\:\:\:{BM}={MF}\:\:\:{BN}={NE} \\ $$$${MN}\mid\mid\:{BC}\:\:\:{MN}={x}+{y} \\ $$$$\bigtriangleup{BFC}\:\:\:\bigtriangleup{BEC}\:{semblables} \\ $$$$\left({meme}\:{cote}\:{BC}\right. \\ $$$$\bigtriangleup{BFC}\:\:\frac{{BM}}{{MF}}=\frac{{BC}}{{x}}\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\bigtriangleup{BEC}\:\:\frac{{CN}}{{NE}}=\frac{{BC}}{{y}}\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${d}'{autre}\:{part}\::\bigtriangleup{ABDet}\:\:\bigtriangleup{ADC}\: \\ $$$$\frac{{AP}}{{PD}}=\frac{{AM}}{{BM}}=\frac{{AN}}{{NB}}\Rightarrow\frac{{x}}{{BD}}=\frac{{y}}{{CD}}\:\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\frac{\left(\mathrm{1}\right)}{\left(\mathrm{2}\right)}=\frac{{y}}{{x}}=\frac{{BM}}{{MF}}×\frac{{NE}}{{NC}} \\ $$$$\frac{{BM}}{{MF}}×\frac{{x}}{{y}}=\frac{{NC}}{{NE}}\:\:\:\:\:\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{3}\right)\:\:\:\:\frac{{x}}{{y}}=\frac{{BD}}{{CD}}\:\:\:\:\:\:\:\left(\mathrm{5}\right) \\ $$$$\frac{\left(\mathrm{4}\right)}{\left(\mathrm{5}\right)}\Rightarrow\frac{{BM}}{{MF}}=\frac{{NC}}{{NE}}×\frac{{CD}}{{BD}} \\ $$$${comme}\:{BM}={MF}\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{BD}={CD} \\ $$$${donc}\:\:\:\:\:\frac{{BM}}{{MF}}=\frac{{x}}{{y}}=\frac{{NC}}{{NE}}=\frac{{NE}}{{NC}}=\frac{{BD}}{{CD}} \\ $$$$\Rightarrow\:\bullet{BM}=\:{MF}\Rightarrow\begin{cases}{{NE}={NC}}\\{\:\:\:\:\:{x}={y}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{et}\:\left({EF}\mid\mid{MN}\mid\mid{BC}\right)\:\: \\ $$
Commented by a.lgnaoui last updated on 12/Mar/23