
Question Number 188998 by SLVR last updated on 10/Mar/23

Commented by SLVR last updated on 10/Mar/23

$${kindly}\:{help}\:{me} \\ $$
Commented by manxsol last updated on 12/Mar/23
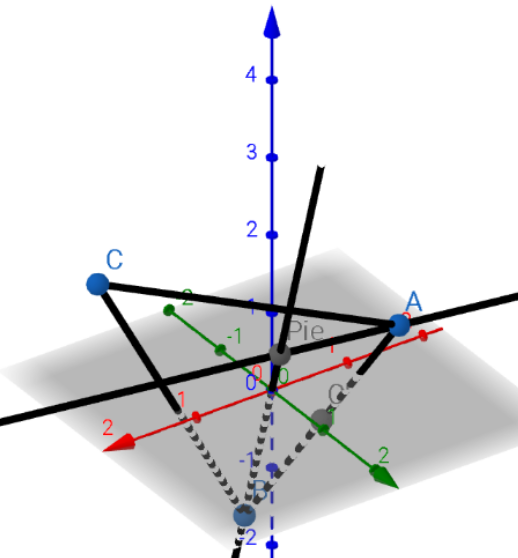
Commented by manxsol last updated on 12/Mar/23
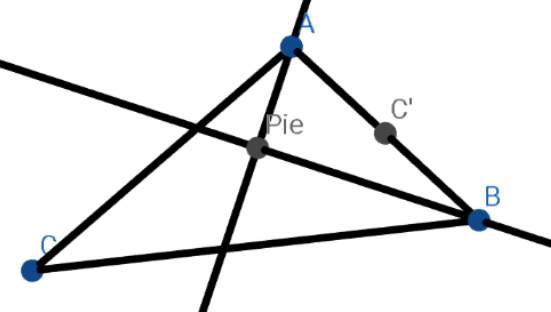
Answered by a.lgnaoui last updated on 10/Mar/23
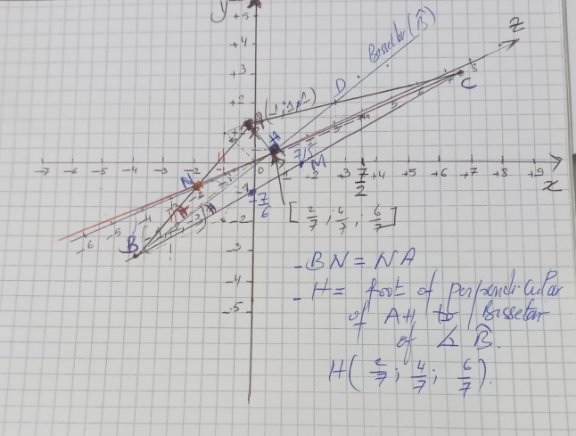
Commented by SLVR last updated on 15/Mar/23
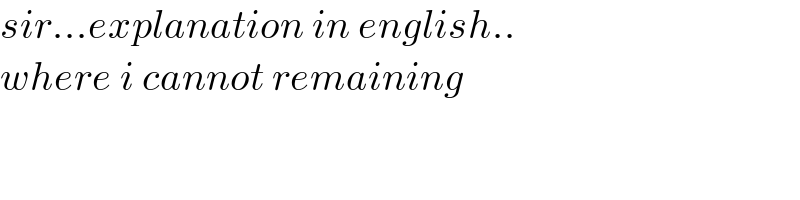
$${sir}...{explanation}\:{in}\:{english}.. \\ $$$${where}\:{i}\:{cannot}\:{remaining} \\ $$
Answered by manxsol last updated on 12/Mar/23
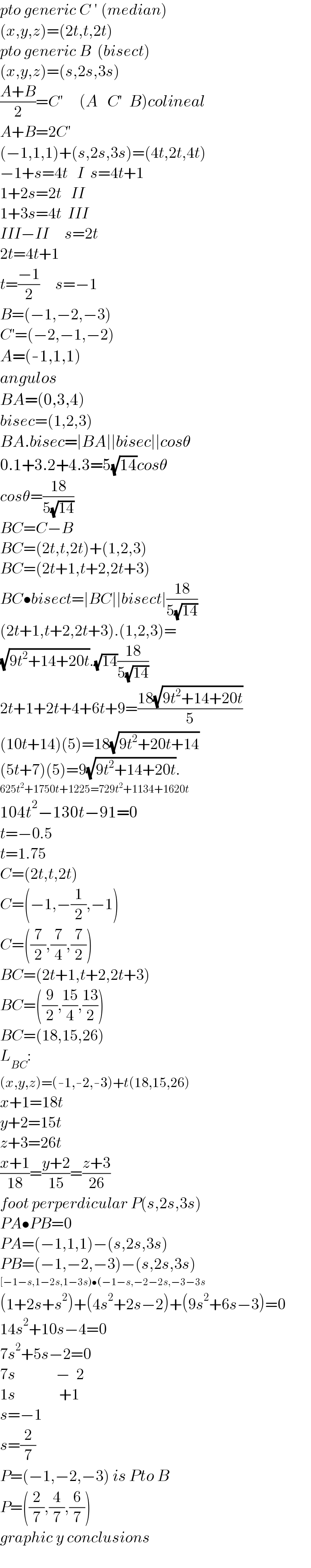
$${pto}\:{generic}\:{C}\:'\:\left({median}\right) \\ $$$$\left({x},{y},{z}\right)=\left(\mathrm{2}{t},{t},\mathrm{2}{t}\right) \\ $$$${pto}\:{generic}\:{B}\:\:\left({bisect}\right) \\ $$$$\left({x},{y},{z}\right)=\left({s},\mathrm{2}{s},\mathrm{3}{s}\right) \\ $$$$\frac{{A}+{B}}{\mathrm{2}}={C}'\:\:\:\:\:\left({A}\:\:\:{C}'\:\:{B}\right){colineal} \\ $$$${A}+{B}=\mathrm{2}{C}' \\ $$$$\left(−\mathrm{1},\mathrm{1},\mathrm{1}\right)+\left({s},\mathrm{2}{s},\mathrm{3}{s}\right)=\left(\mathrm{4}{t},\mathrm{2}{t},\mathrm{4}{t}\right) \\ $$$$−\mathrm{1}+{s}=\mathrm{4}{t}\:\:\:{I}\:\:{s}=\mathrm{4}{t}+\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{2}{s}=\mathrm{2}{t}\:\:\:{II} \\ $$$$\mathrm{1}+\mathrm{3}{s}=\mathrm{4}{t}\:\:{III} \\ $$$${III}−{II}\:\:\:\:\:{s}=\mathrm{2}{t} \\ $$$$\mathrm{2}{t}=\mathrm{4}{t}+\mathrm{1} \\ $$$${t}=\frac{−\mathrm{1}}{\mathrm{2}}\:\:\:\:\:{s}=−\mathrm{1} \\ $$$${B}=\left(−\mathrm{1},−\mathrm{2},−\mathrm{3}\right) \\ $$$${C}'=\left(−\mathrm{2},−\mathrm{1},−\mathrm{2}\right) \\ $$$${A}=\left(-\mathrm{1},\mathrm{1},\mathrm{1}\right) \\ $$$${angulos} \\ $$$${BA}=\left(\mathrm{0},\mathrm{3},\mathrm{4}\right) \\ $$$${bisec}=\left(\mathrm{1},\mathrm{2},\mathrm{3}\right) \\ $$$${BA}.{bisec}=\mid{BA}\mid\mid{bisec}\mid\mid{cos}\theta \\ $$$$\mathrm{0}.\mathrm{1}+\mathrm{3}.\mathrm{2}+\mathrm{4}.\mathrm{3}=\mathrm{5}\sqrt{\mathrm{14}}{cos}\theta \\ $$$${cos}\theta=\frac{\mathrm{18}}{\mathrm{5}\sqrt{\mathrm{14}}} \\ $$$${BC}={C}−{B} \\ $$$${BC}=\left(\mathrm{2}{t},{t},\mathrm{2}{t}\right)+\left(\mathrm{1},\mathrm{2},\mathrm{3}\right) \\ $$$${BC}=\left(\mathrm{2}{t}+\mathrm{1},{t}+\mathrm{2},\mathrm{2}{t}+\mathrm{3}\right) \\ $$$${BC}\bullet{bisect}=\mid{BC}\mid\mid{bisect}\mid\frac{\mathrm{18}}{\mathrm{5}\sqrt{\mathrm{14}}} \\ $$$$\left(\mathrm{2}{t}+\mathrm{1},{t}+\mathrm{2},\mathrm{2}{t}+\mathrm{3}\right).\left(\mathrm{1},\mathrm{2},\mathrm{3}\right)= \\ $$$$\sqrt{\mathrm{9}{t}^{\mathrm{2}} +\mathrm{14}+\mathrm{20}{t}}.\sqrt{\mathrm{14}}\frac{\mathrm{18}}{\mathrm{5}\sqrt{\mathrm{14}}} \\ $$$$\mathrm{2}{t}+\mathrm{1}+\mathrm{2}{t}+\mathrm{4}+\mathrm{6}{t}+\mathrm{9}=\frac{\mathrm{18}\sqrt{\mathrm{9}{t}^{\mathrm{2}} +\mathrm{14}+\mathrm{20}{t}}}{\mathrm{5}} \\ $$$$\left(\mathrm{10}{t}+\mathrm{14}\right)\left(\mathrm{5}\right)=\mathrm{18}\sqrt{\mathrm{9}{t}^{\mathrm{2}} +\mathrm{20}{t}+\mathrm{14}} \\ $$$$\left(\mathrm{5}{t}+\mathrm{7}\right)\left(\mathrm{5}\right)=\mathrm{9}\sqrt{\mathrm{9}{t}^{\mathrm{2}} +\mathrm{14}+\mathrm{20}{t}}. \\ $$$$\mathrm{625}{t}^{\mathrm{2}} +\mathrm{1750}{t}+\mathrm{1225}=\mathrm{729}{t}^{\mathrm{2}} +\mathrm{1134}+\mathrm{1620}{t} \\ $$$$\mathrm{104}{t}^{\mathrm{2}} −\mathrm{130}{t}−\mathrm{91}=\mathrm{0} \\ $$$${t}=−\mathrm{0}.\mathrm{5} \\ $$$${t}=\mathrm{1}.\mathrm{75} \\ $$$${C}=\left(\mathrm{2}{t},{t},\mathrm{2}{t}\right) \\ $$$${C}=\left(−\mathrm{1},−\frac{\mathrm{1}}{\mathrm{2}},−\mathrm{1}\right) \\ $$$${C}=\left(\frac{\mathrm{7}}{\mathrm{2}},\frac{\mathrm{7}}{\mathrm{4}},\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$$${BC}=\left(\mathrm{2}{t}+\mathrm{1},{t}+\mathrm{2},\mathrm{2}{t}+\mathrm{3}\right) \\ $$$${BC}=\left(\frac{\mathrm{9}}{\mathrm{2}},\frac{\mathrm{15}}{\mathrm{4}},\frac{\mathrm{13}}{\mathrm{2}}\right) \\ $$$${BC}=\left(\mathrm{18},\mathrm{15},\mathrm{26}\right) \\ $$$${L}_{{BC}} :\: \\ $$$$\left({x},{y},{z}\right)=\left(-\mathrm{1},-\mathrm{2},-\mathrm{3}\right)+{t}\left(\mathrm{18},\mathrm{15},\mathrm{26}\right) \\ $$$${x}+\mathrm{1}=\mathrm{18}{t} \\ $$$${y}+\mathrm{2}=\mathrm{15}{t} \\ $$$${z}+\mathrm{3}=\mathrm{26}{t} \\ $$$$\frac{{x}+\mathrm{1}}{\mathrm{18}}=\frac{{y}+\mathrm{2}}{\mathrm{15}}=\frac{{z}+\mathrm{3}}{\mathrm{26}} \\ $$$${foot}\:{perperdicular}\:{P}\left({s},\mathrm{2}{s},\mathrm{3}{s}\right) \\ $$$${PA}\bullet{PB}=\mathrm{0} \\ $$$${PA}=\left(−\mathrm{1},\mathrm{1},\mathrm{1}\right)−\left({s},\mathrm{2}{s},\mathrm{3}{s}\right) \\ $$$${PB}=\left(−\mathrm{1},−\mathrm{2},−\mathrm{3}\right)−\left({s},\mathrm{2}{s},\mathrm{3}{s}\right) \\ $$$$\left[−\mathrm{1}−{s},\mathrm{1}−\mathrm{2}{s},\mathrm{1}−\mathrm{3}{s}\right)\bullet\left(−\mathrm{1}−{s},−\mathrm{2}−\mathrm{2}{s},−\mathrm{3}−\mathrm{3}{s}\right. \\ $$$$\left(\mathrm{1}+\mathrm{2}{s}+{s}^{\mathrm{2}} \right)+\left(\mathrm{4}{s}^{\mathrm{2}} +\mathrm{2}{s}−\mathrm{2}\right)+\left(\mathrm{9}{s}^{\mathrm{2}} +\mathrm{6}{s}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{14}{s}^{\mathrm{2}} +\mathrm{10}{s}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{7}{s}^{\mathrm{2}} +\mathrm{5}{s}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{7}{s}\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\mathrm{2} \\ $$$$\mathrm{1}{s}\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{1} \\ $$$${s}=−\mathrm{1} \\ $$$${s}=\frac{\mathrm{2}}{\mathrm{7}} \\ $$$${P}=\left(−\mathrm{1},−\mathrm{2},−\mathrm{3}\right)\:{is}\:{Pto}\:{B} \\ $$$${P}=\left(\frac{\mathrm{2}}{\mathrm{7}},\frac{\mathrm{4}}{\mathrm{7}},\frac{\mathrm{6}}{\mathrm{7}}\right) \\ $$$${graphic}\:{y}\:{conclusions} \\ $$$$ \\ $$
Commented by SLVR last updated on 15/Mar/23
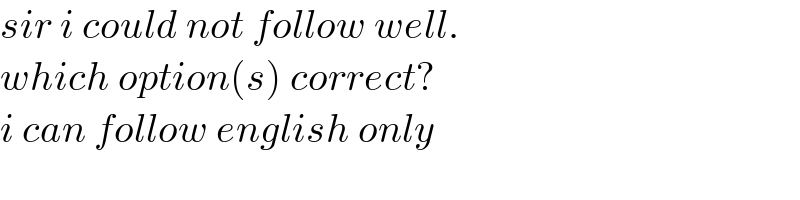
$${sir}\:{i}\:{could}\:{not}\:{follow}\:{well}. \\ $$$${which}\:{option}\left({s}\right)\:{correct}? \\ $$$${i}\:{can}\:{follow}\:{english}\:{only} \\ $$
