Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 188912 by Mingma last updated on 08/Mar/23

Answered by a.lgnaoui last updated on 09/Mar/23

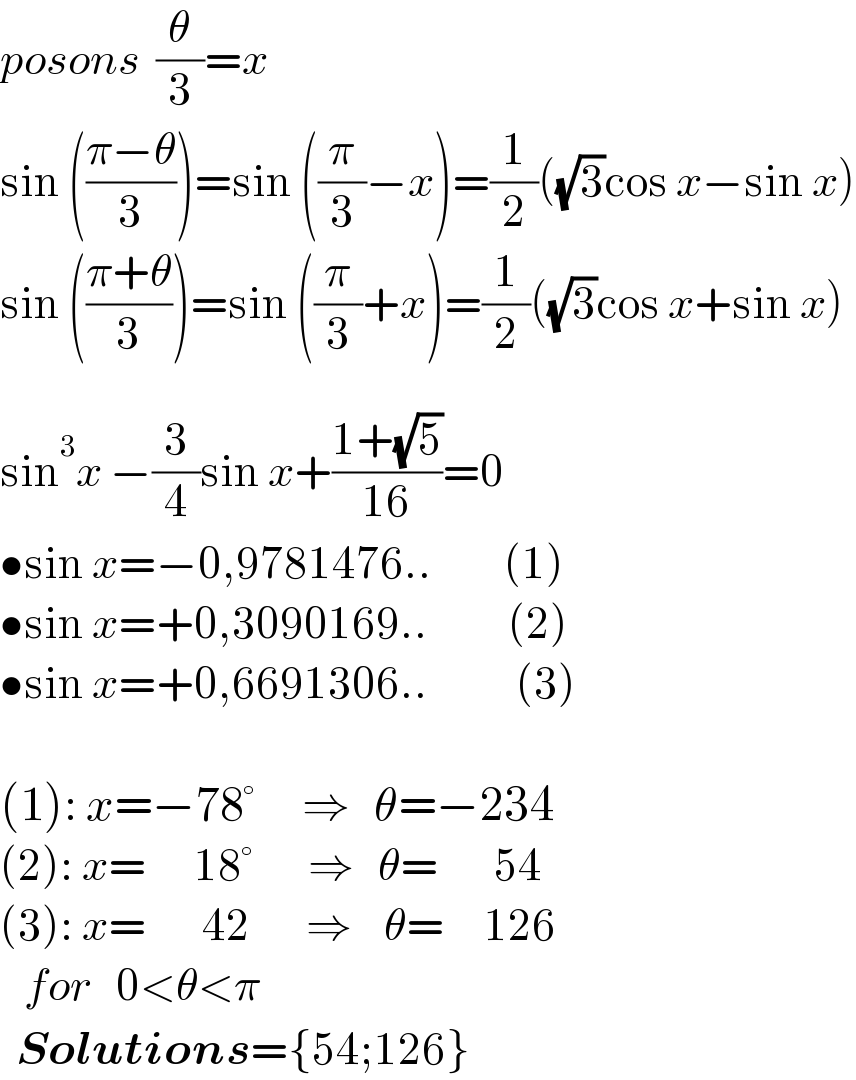
posons (θ/3)=x sin (((π−θ)/3))=sin ((π/3)−x)=(1/2)((√3)cos x−sin x) sin (((π+θ)/3))=sin ((π/3)+x)=(1/2)((√3)cos x+sin x) sin^3 x −(3/4)sin x+((1+(√5))/(16))=0 •sin x=−0,9781476.. (1) •sin x=+0,3090169.. (2) •sin x=+0,6691306.. (3) (1): x=−78° ⇒ θ=−234 (2): x= 18° ⇒ θ= 54 (3): x= 42 ⇒ θ= 126 for 0<θ<π Solutions={54;126}

$${posons}\:\:\frac{\theta}{\mathrm{3}}={x} \\ $$$$\mathrm{sin}\:\left(\frac{\pi−\theta}{\mathrm{3}}\right)=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right) \\ $$$$\mathrm{sin}\:\left(\frac{\pi+\theta}{\mathrm{3}}\right)=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right) \\ $$$$\:\: \\ $$$$\mathrm{sin}^{\mathrm{3}} {x}\:−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}\:{x}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{16}}=\mathrm{0} \\ $$$$\bullet\mathrm{sin}\:{x}=−\mathrm{0},\mathrm{9781476}..\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\bullet\mathrm{sin}\:{x}=+\mathrm{0},\mathrm{3090169}..\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\bullet\mathrm{sin}\:{x}=+\mathrm{0},\mathrm{6691306}..\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right):\:{x}=−\mathrm{78}°\:\:\:\:\:\:\Rightarrow\:\:\:\theta=−\mathrm{234} \\ $$$$\left(\mathrm{2}\right):\:{x}=\:\:\:\:\:\:\mathrm{18}°\:\:\:\:\:\:\:\Rightarrow\:\:\:\theta=\:\:\:\:\:\:\:\mathrm{54} \\ $$$$\left(\mathrm{3}\right):\:{x}=\:\:\:\:\:\:\:\mathrm{42}\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\theta=\:\:\:\:\:\mathrm{126} \\ $$$$\:\:\:{for}\:\:\:\mathrm{0}<\theta<\pi \\ $$$$\:\:\boldsymbol{{Solutions}}=\left\{\mathrm{54};\mathrm{126}\right\}\:\: \\ $$

Commented by a.lgnaoui last updated on 08/Mar/23

Commented by Mingma last updated on 09/Mar/23

Excellent!

Answered by mr W last updated on 09/Mar/23

recall sin α sin β=(1/2)[cos (α−β)−cos (α+β)] sin 3x=sin x(3−4 sin^2 x) sin 54°=sin ((3π)/(10))=((1+(√5))/4) let x=(θ/3) sin ((π/3)−x) sin ((π/3)+x) =(1/2)[cos (−2x)−cos ((2π)/3)] =(1/2)[cos (2x)+(1/2)] =(1/4)(3−4 sin^2 x) eqn. becomes to (1/4)(3−4 sin^2 x)sin x=((1+(√5))/(16)) (3−4 sin^2 x)sin x=((1+(√5))/4) sin 3x=((1+(√5))/4) sin θ=((1+(√5))/4) ⇒θ=nπ+(−1)^n sin^(−1) ((1+(√5))/4) ⇒θ=nπ+(((−1)^n 3π)/(10)) within 0<θ<π ⇒θ=((3π)/(10)) or ((7π)/(10)), i.e. 54° or 126°

$${recall}\: \\ $$$$\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{cos}\:\left(\alpha−\beta\right)−\mathrm{cos}\:\left(\alpha+\beta\right)\right] \\ $$$$\mathrm{sin}\:\mathrm{3}{x}=\mathrm{sin}\:{x}\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right) \\ $$$$\mathrm{sin}\:\mathrm{54}°=\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{10}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$ \\ $$$${let}\:{x}=\frac{\theta}{\mathrm{3}} \\ $$$$\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−{x}\right)\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{cos}\:\left(−\mathrm{2}{x}\right)−\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{cos}\:\left(\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right) \\ $$$${eqn}.\:{becomes}\:{to} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)\mathrm{sin}\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)\mathrm{sin}\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\mathrm{3}{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow\theta={n}\pi+\left(−\mathrm{1}\right)^{{n}} \:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow\theta={n}\pi+\frac{\left(−\mathrm{1}\right)^{{n}} \mathrm{3}\pi}{\mathrm{10}}\: \\ $$$${within}\:\mathrm{0}<\theta<\pi \\ $$$$\Rightarrow\theta=\frac{\mathrm{3}\pi}{\mathrm{10}}\:{or}\:\frac{\mathrm{7}\pi}{\mathrm{10}},\:{i}.{e}.\:\mathrm{54}°\:{or}\:\mathrm{126}° \\ $$

Commented by manxsol last updated on 09/Mar/23

Clear job. Perfect!

$${Clear}\:{job}.\:{Perfect}! \\ $$

Answered by Frix last updated on 09/Mar/23

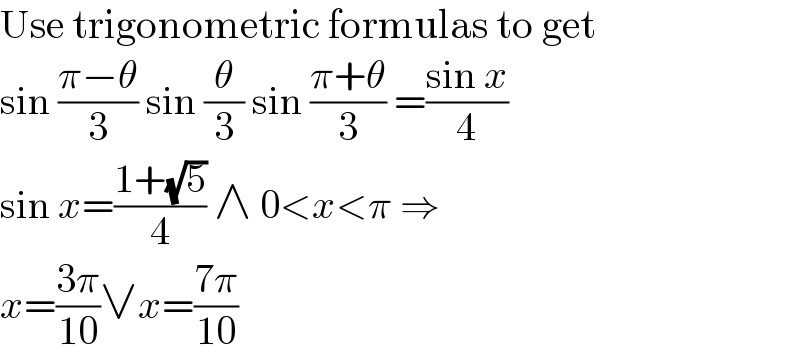
Use trigonometric formulas to get sin ((π−θ)/3) sin (θ/3) sin ((π+θ)/3) =((sin x)/4) sin x=((1+(√5))/4) ∧ 0<x<π ⇒ x=((3π)/(10))∨x=((7π)/(10))

$$\mathrm{Use}\:\mathrm{trigonometric}\:\mathrm{formulas}\:\mathrm{to}\:\mathrm{get} \\ $$$$\mathrm{sin}\:\frac{\pi−\theta}{\mathrm{3}}\:\mathrm{sin}\:\frac{\theta}{\mathrm{3}}\:\mathrm{sin}\:\frac{\pi+\theta}{\mathrm{3}}\:=\frac{\mathrm{sin}\:{x}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\:\wedge\:\mathrm{0}<{x}<\pi\:\Rightarrow \\ $$$${x}=\frac{\mathrm{3}\pi}{\mathrm{10}}\vee{x}=\frac{\mathrm{7}\pi}{\mathrm{10}} \\ $$

Answered by mnjuly1970 last updated on 09/Mar/23

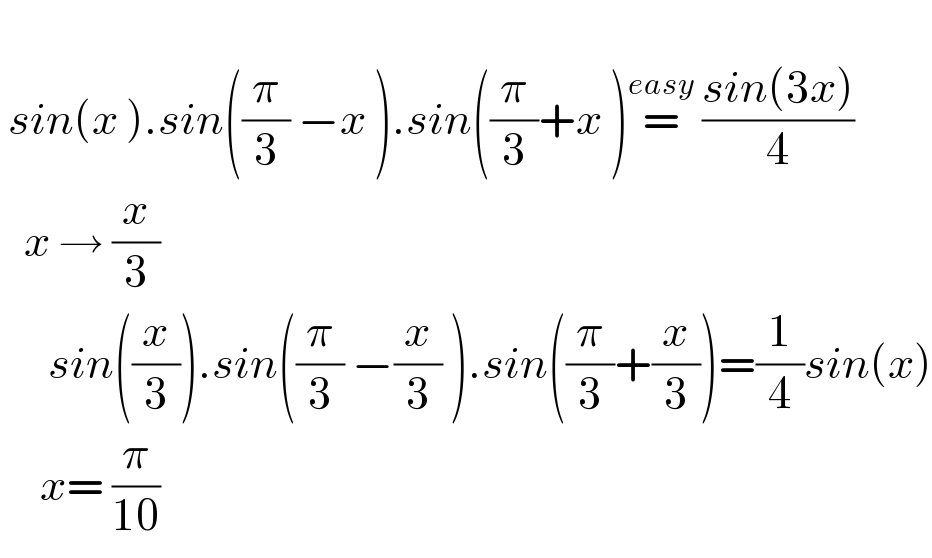
sin(x ).sin((π/3) −x ).sin((π/3)+x )=^(easy) ((sin(3x))/4) x → (x/3) sin((x/3)).sin((π/3) −(x/3) ).sin((π/3)+(x/3))=(1/4)sin(x) x= (π/(10))

$$ \\ $$$$\:{sin}\left({x}\:\right).{sin}\left(\frac{\pi}{\mathrm{3}}\:−{x}\:\right).{sin}\left(\frac{\pi}{\mathrm{3}}+{x}\:\right)\overset{{easy}} {=}\:\frac{{sin}\left(\mathrm{3}{x}\right)}{\mathrm{4}} \\ $$$$\:\:\:{x}\:\rightarrow\:\frac{{x}}{\mathrm{3}} \\ $$$$\:\:\:\:\:\:{sin}\left(\frac{{x}}{\mathrm{3}}\right).{sin}\left(\frac{\pi}{\mathrm{3}}\:−\frac{{x}}{\mathrm{3}}\:\right).{sin}\left(\frac{\pi}{\mathrm{3}}+\frac{{x}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{4}}{sin}\left({x}\right) \\ $$$$\:\:\:\:\:{x}=\:\frac{\pi}{\mathrm{10}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com