
Question Number 188819 by mnjuly1970 last updated on 07/Mar/23
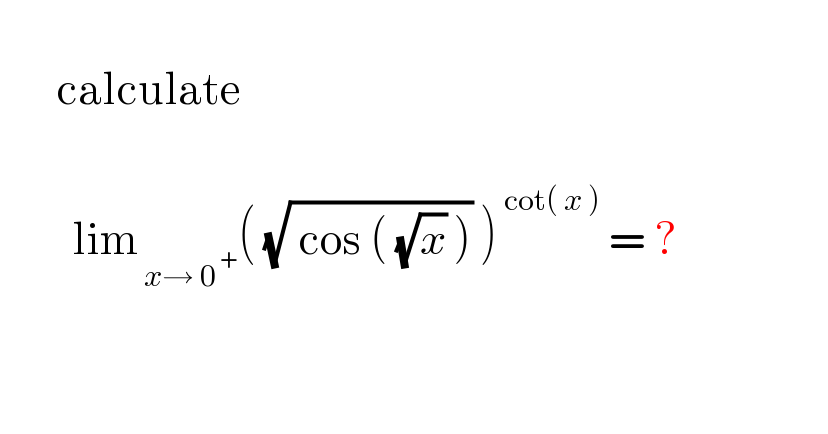
$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{calculate}\: \\ $$$$\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{lim}_{\:{x}\rightarrow\:\mathrm{0}^{\:+} } \left(\:\sqrt{\:\mathrm{cos}\:\left(\:\sqrt{{x}}\:\right)}\:\right)^{\:\mathrm{cot}\left(\:{x}\:\right)} \:=\:?\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$
Commented by mehdee42 last updated on 07/Mar/23

$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{calculate}\: \\ $$$$\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{lim}_{\:{x}\rightarrow\:\mathrm{0}^{\:+} } \left(\:\sqrt{\:\mathrm{cos}\:\left(\:\sqrt{{x}}\:\right)}\:\right)^{\:\mathrm{cot}\left(\:{x}\:\right)} \:=\:?\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$$${notic} \\ $$$${if}\:{lim}_{{x}\rightarrow{a}} {f}\left({x}\right)=\mathrm{1}\:\&\:{lim}_{{x}\rightarrow{a}} {g}\left({x}\right)=\infty \\ $$$$\Rightarrow{lim}_{{x}\rightarrow{a}} {f}\left({x}\right)^{{g}\left({x}\right)} ={e}^{{lim}_{{x}\rightarrow{a}} \left({f}\left({x}\right)−\mathrm{1}\right){g}\left({x}\right)} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{+} } \frac{\sqrt{{cos}\sqrt{{x}}}−\mathrm{1}}{{tanx}}\overset{{hop}} {=}{lim}_{{x}\rightarrow{a}} \frac{\frac{−{sin}\sqrt{{x}}}{\mathrm{2}\sqrt{{x}}}}{\mathrm{2}\left(\mathrm{1}+{tanx}\right)\sqrt{{cos}\sqrt{{x}}}}=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{answr}\:{is}\::\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{{e}}} \\ $$$$ \\ $$
Answered by mahdipoor last updated on 07/Mar/23
![y=((√(cos((√x)))))^(cot(x)) =[cos((√x))]^((cot(x))/2) ⇒ln(y)=((cot(x))/2)ln(cos((√x)))=((ln(cos((√x))))/(2tan(x))) ⇒x→0^+ lim[ln(y)]=lim((ln(cos(√x)))/(2tan(x))) ⇒=(0/0) , Hop ⇒=((((−sin((√x)))/(cos((√x)))).(1/(2(√x))))/(2/(cos^2 (x))))= ((−cos^2 (x))/(4cos((√x))))×[((sin((√x)))/( (√x)))]=((−1)/4)×((sin(√x))/( (√x))) ⇒hop ⇒((cos((√x))×(1/(2(√x))))/(1/(2(√x))))=cos(√x)=1 ⇒⇒lim ln(y)=((−1)/4)×1 ⇒lim y=(1/(^4 (√e))) ...............Note: get lim x→c ((f(x))/(g(x)))= , f(c)=g(c)=0 ((f(x))/(g(x)))=k(x)((u(x))/(v(x))) that k(c)≠0,u(c)=v(c)=0 ⇒ hop ⇒ ((k^′ (c)u(c)+k(c)u^′ (c))/(v^′ (c)))=k(c)((u^′ (c))/(v^′ (c))) ...............](Q188823.png)
$${y}=\left(\sqrt{{cos}\left(\sqrt{{x}}\right)}\right)^{{cot}\left({x}\right)} =\left[{cos}\left(\sqrt{{x}}\right)\right]^{\frac{{cot}\left({x}\right)}{\mathrm{2}}} \\ $$$$\Rightarrow{ln}\left({y}\right)=\frac{{cot}\left({x}\right)}{\mathrm{2}}{ln}\left({cos}\left(\sqrt{{x}}\right)\right)=\frac{{ln}\left({cos}\left(\sqrt{{x}}\right)\right)}{\mathrm{2}{tan}\left({x}\right)} \\ $$$$\Rightarrow{x}\rightarrow\mathrm{0}^{+} \:\:\:{lim}\left[{ln}\left({y}\right)\right]={lim}\frac{{ln}\left({cos}\sqrt{{x}}\right)}{\mathrm{2}{tan}\left({x}\right)} \\ $$$$\Rightarrow=\frac{\mathrm{0}}{\mathrm{0}}\:,\:{Hop}\:\Rightarrow=\frac{\frac{−{sin}\left(\sqrt{{x}}\right)}{{cos}\left(\sqrt{{x}}\right)}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\frac{\mathrm{2}}{{cos}^{\mathrm{2}} \left({x}\right)}}= \\ $$$$\frac{−{cos}^{\mathrm{2}} \left({x}\right)}{\mathrm{4}{cos}\left(\sqrt{{x}}\right)}×\left[\frac{{sin}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\right]=\frac{−\mathrm{1}}{\mathrm{4}}×\frac{{sin}\sqrt{{x}}}{\:\sqrt{{x}}} \\ $$$$\Rightarrow{hop}\:\Rightarrow\frac{{cos}\left(\sqrt{{x}}\right)×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}={cos}\sqrt{{x}}=\mathrm{1} \\ $$$$\Rightarrow\Rightarrow{lim}\:\:\:\:{ln}\left({y}\right)=\frac{−\mathrm{1}}{\mathrm{4}}×\mathrm{1}\:\:\Rightarrow{lim}\:\:\:{y}=\frac{\mathrm{1}}{\:^{\mathrm{4}} \sqrt{{e}}} \\ $$$$...............{Note}:\:\: \\ $$$${get}\:{lim}\:\:{x}\rightarrow{c}\:\:\:\frac{{f}\left({x}\right)}{{g}\left({x}\right)}=\:\:\:,\:\:\:{f}\left({c}\right)={g}\left({c}\right)=\mathrm{0} \\ $$$$\frac{{f}\left({x}\right)}{{g}\left({x}\right)}={k}\left({x}\right)\frac{{u}\left({x}\right)}{{v}\left({x}\right)}\:\:{that}\:\:\:{k}\left({c}\right)\neq\mathrm{0},{u}\left({c}\right)={v}\left({c}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{hop}\:\Rightarrow\:\frac{{k}^{'} \left({c}\right){u}\left({c}\right)+{k}\left({c}\right){u}^{'} \left({c}\right)}{{v}^{'} \left({c}\right)}={k}\left({c}\right)\frac{{u}^{'} \left({c}\right)}{{v}^{'} \left({c}\right)} \\ $$$$............... \\ $$
Commented by mnjuly1970 last updated on 07/Mar/23

$${sepas}\:{ostad} \\ $$
Answered by qaz last updated on 07/Mar/23
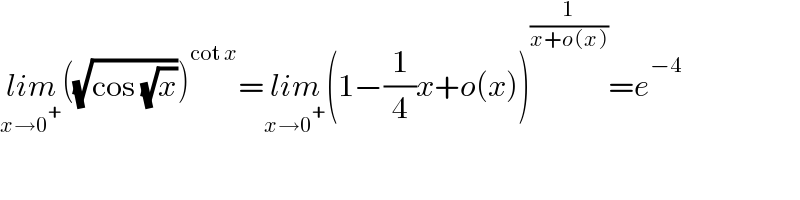
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}}\left(\sqrt{\mathrm{cos}\:\sqrt{{x}}}\right)^{\mathrm{cot}\:{x}} =\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}{x}+{o}\left({x}\right)\right)^{\frac{\mathrm{1}}{{x}+{o}\left({x}\right)}} ={e}^{−\mathrm{4}} \\ $$
