
Question Number 188774 by Shrinava last updated on 06/Mar/23
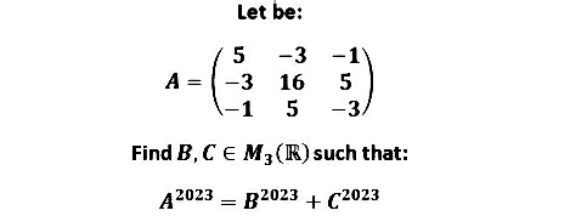
Answered by aleks041103 last updated on 09/Mar/23
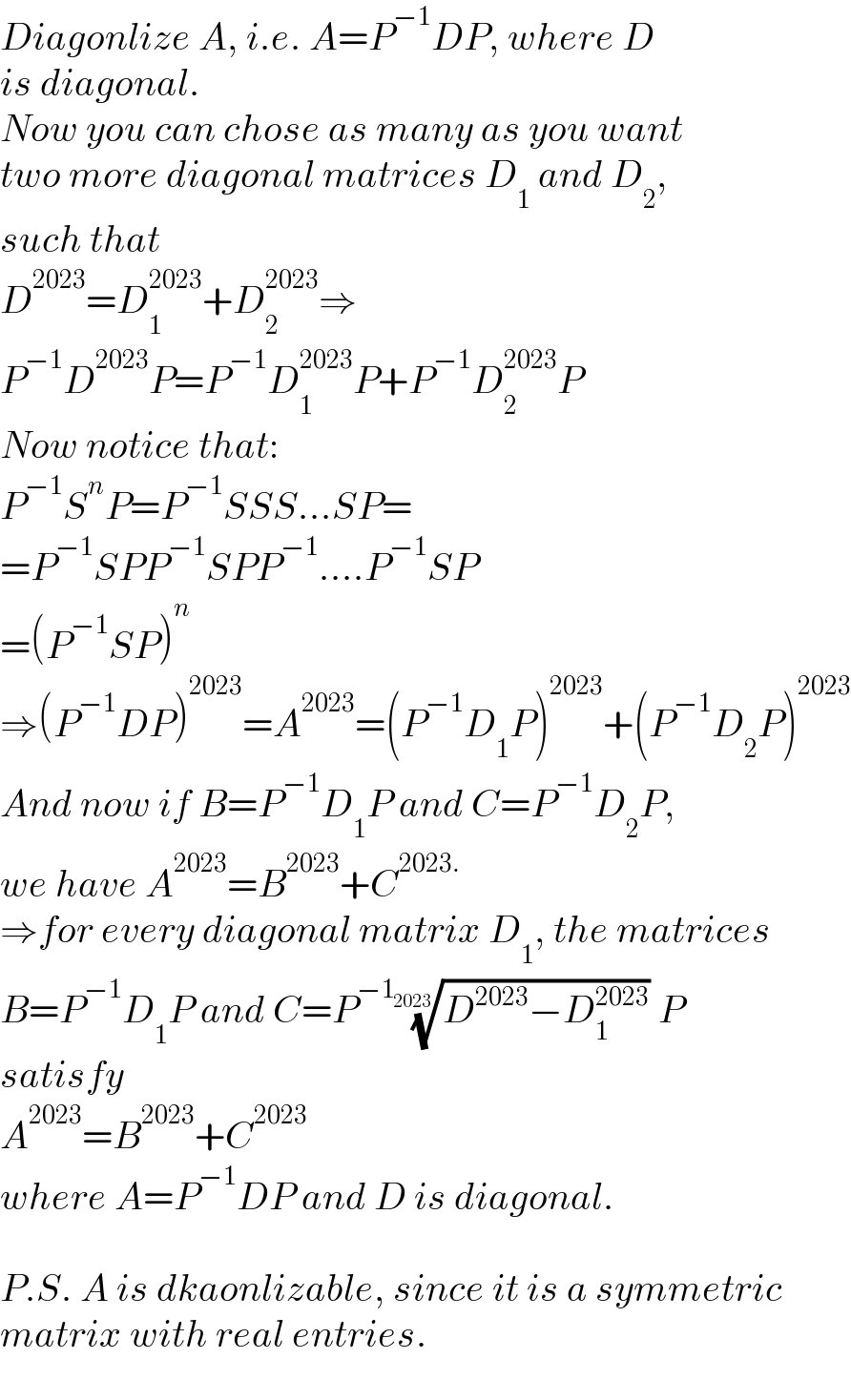
$${Diagonlize}\:{A},\:{i}.{e}.\:{A}={P}^{−\mathrm{1}} {DP},\:{where}\:{D} \\ $$$${is}\:{diagonal}. \\ $$$${Now}\:{you}\:{can}\:{chose}\:{as}\:{many}\:{as}\:{you}\:{want} \\ $$$${two}\:{more}\:{diagonal}\:{matrices}\:{D}_{\mathrm{1}} \:{and}\:{D}_{\mathrm{2}} , \\ $$$${such}\:{that} \\ $$$${D}^{\mathrm{2023}} ={D}_{\mathrm{1}} ^{\mathrm{2023}} +{D}_{\mathrm{2}} ^{\mathrm{2023}} \Rightarrow \\ $$$${P}^{−\mathrm{1}} {D}^{\mathrm{2023}} {P}={P}^{−\mathrm{1}} {D}_{\mathrm{1}} ^{\mathrm{2023}} {P}+{P}^{−\mathrm{1}} {D}_{\mathrm{2}} ^{\mathrm{2023}} {P} \\ $$$${Now}\:{notice}\:{that}: \\ $$$${P}^{−\mathrm{1}} {S}^{{n}} {P}={P}^{−\mathrm{1}} {SSS}...{SP}= \\ $$$$={P}^{−\mathrm{1}} {SPP}^{−\mathrm{1}} {SPP}^{−\mathrm{1}} ....{P}^{−\mathrm{1}} {SP} \\ $$$$=\left({P}^{−\mathrm{1}} {SP}\right)^{{n}} \\ $$$$\Rightarrow\left({P}^{−\mathrm{1}} {DP}\right)^{\mathrm{2023}} ={A}^{\mathrm{2023}} =\left({P}^{−\mathrm{1}} {D}_{\mathrm{1}} {P}\right)^{\mathrm{2023}} +\left({P}^{−\mathrm{1}} {D}_{\mathrm{2}} {P}\right)^{\mathrm{2023}} \\ $$$${And}\:{now}\:{if}\:{B}={P}^{−\mathrm{1}} {D}_{\mathrm{1}} {P}\:{and}\:{C}={P}^{−\mathrm{1}} {D}_{\mathrm{2}} {P}, \\ $$$${we}\:{have}\:{A}^{\mathrm{2023}} ={B}^{\mathrm{2023}} +{C}^{\mathrm{2023}.} \\ $$$$\Rightarrow{for}\:{every}\:{diagonal}\:{matrix}\:{D}_{\mathrm{1}} ,\:{the}\:{matrices} \\ $$$${B}={P}^{−\mathrm{1}} {D}_{\mathrm{1}} {P}\:{and}\:{C}={P}^{−\mathrm{1}} \sqrt[{\mathrm{2023}}]{{D}^{\mathrm{2023}} −{D}_{\mathrm{1}} ^{\mathrm{2023}} }{P} \\ $$$${satisfy} \\ $$$${A}^{\mathrm{2023}} ={B}^{\mathrm{2023}} +{C}^{\mathrm{2023}} \\ $$$${where}\:{A}={P}^{−\mathrm{1}} {DP}\:{and}\:{D}\:{is}\:{diagonal}. \\ $$$$ \\ $$$${P}.{S}.\:{A}\:{is}\:{dkaonlizable},\:{since}\:{it}\:{is}\:{a}\:{symmetric} \\ $$$${matrix}\:{with}\:{real}\:{entries}. \\ $$
Commented by Shrinava last updated on 09/Mar/23

$$\mathrm{Dear}\:\mathrm{professor},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$$$\mathrm{the}\:\mathrm{for}\:\mathrm{detailed}\:\mathrm{explanation}.. \\ $$$$\mathrm{Let}'\mathrm{s}\:\mathrm{note}\:\mathrm{how}\:\mathrm{in}\:\mathrm{response}.? \\ $$
