
Question Number 188704 by mathlove last updated on 05/Mar/23
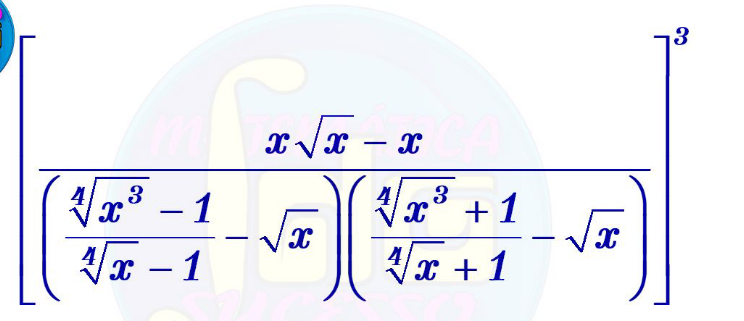
Answered by a.lgnaoui last updated on 05/Mar/23
![posons Z= avec:A=x(√x) −x =x((√x) −1) B= (((x^3 )^(1/4) −1)/( (x)^(1/4) −1)) −(√x) C=((((x^3 ))^(1/4) +1)/( (x)^(1/4) +1))−(√(x )) B=(( (√x) −1 )/( (x)^(1/4) −1)) C=((1−(√x))/( (x)^(1/4) +1)) B×C=1−(√x) ⇒ (A/(B×C))=((x((√x) −1))/( (√x) −1)) Z^3 =(((x(√x) −1)/(1−(√x))))^3 = [((x(√x) −x)/(((((x^3 )^(1/4) −1)/( (x)^(1/4) −1))−(√x) )((((x^3 )^(1/4) +1)/( (x)^(1/4) +1))−(√x) )))]^3 =−x^3 .](Q188715.png)
$${posons}\:\:\:{Z}=\:\:{avec}:{A}={x}\sqrt{{x}}\:−{x}\:\:={x}\left(\sqrt{{x}}\:\:−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:{B}=\:\frac{\sqrt[{\mathrm{4}}]{{x}^{\mathrm{3}} }\:−\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{{x}}\:−\mathrm{1}}\:\:\:−\sqrt{{x}}\:\:\:\:\:\:\:{C}=\frac{\sqrt[{\mathrm{4}}]{{x}^{\mathrm{3}} \:}\:+\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}}−\sqrt{{x}\:}\: \\ $$$${B}=\frac{\:\:\sqrt{{x}}\:−\mathrm{1}\:}{\:\sqrt[{\mathrm{4}}]{{x}}\:−\mathrm{1}}\:\:{C}=\frac{\mathrm{1}−\sqrt{{x}}}{\:\sqrt[{\mathrm{4}}]{{x}}\:+\mathrm{1}}\:\:{B}×{C}=\mathrm{1}−\sqrt{{x}}\: \\ $$$$\Rightarrow\:\frac{{A}}{{B}×{C}}=\frac{{x}\left(\sqrt{{x}}\:−\mathrm{1}\right)}{\:\sqrt{{x}}\:−\mathrm{1}}\:\:\:\: \\ $$$${Z}^{\mathrm{3}} =\left(\frac{\boldsymbol{{x}}\sqrt{\boldsymbol{{x}}}\:−\mathrm{1}}{\mathrm{1}−\sqrt{\boldsymbol{{x}}}}\right)^{\mathrm{3}} = \\ $$$$ \\ $$$$\left[\frac{\boldsymbol{{x}}\sqrt{\boldsymbol{{x}}}\:−\boldsymbol{{x}}}{\left(\frac{\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}^{\mathrm{3}} }\:−\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}}\:−\mathrm{1}}−\sqrt{\boldsymbol{{x}}}\:\right)\left(\frac{\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}^{\mathrm{3}} }\:+\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\boldsymbol{{x}}}\:+\mathrm{1}}−\sqrt{\boldsymbol{{x}}}\:\right)}\right]^{\mathrm{3}} =−\boldsymbol{{x}}^{\mathrm{3}} . \\ $$
Commented by mathlove last updated on 06/Mar/23

$${thanks} \\ $$
