
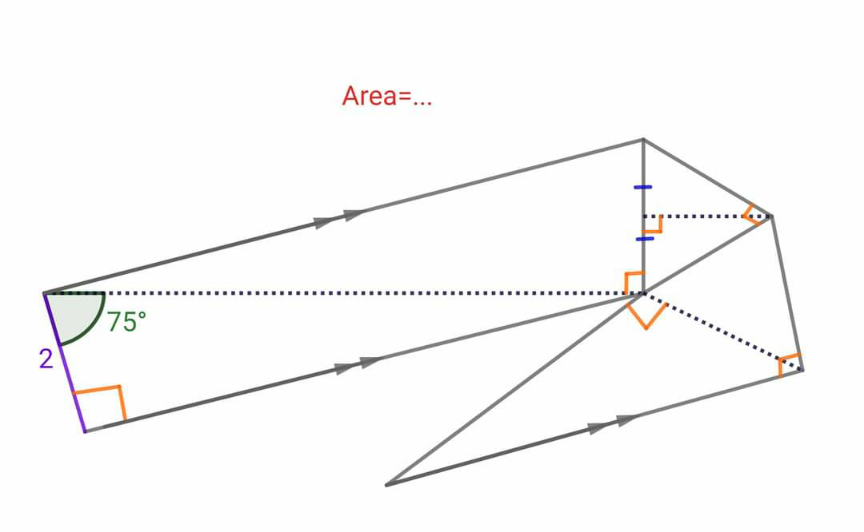
Question Number 188623 by normans last updated on 03/Mar/23
Commented by mr W last updated on 04/Mar/23
Commented by mr W last updated on 04/Mar/23
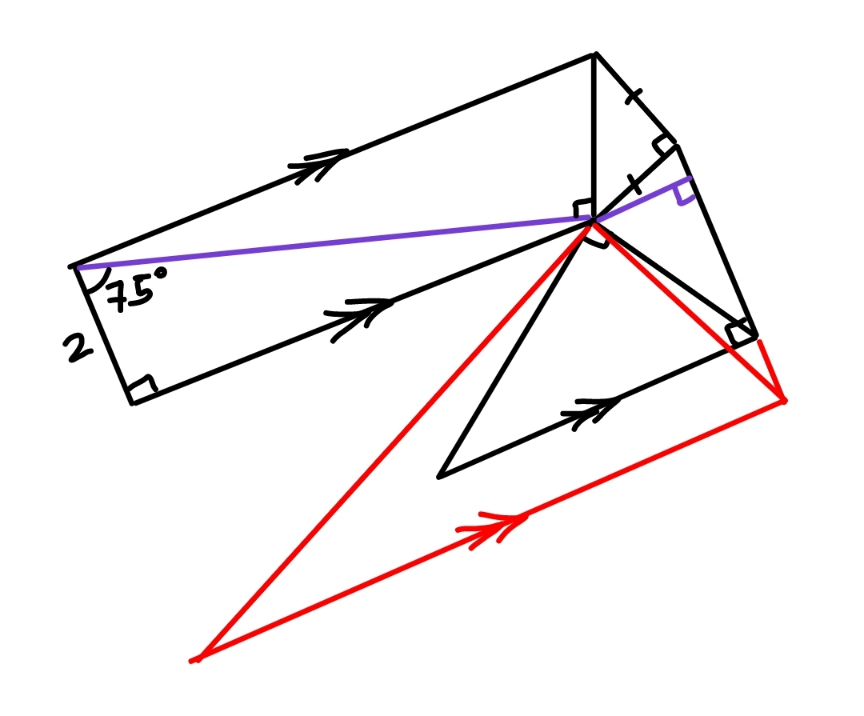
$${data}\:{are}\:{not}\:{sufficient}\:{to}\:{determine} \\ $$$${the}\:{total}\:{area}! \\ $$
Commented by HeferH last updated on 05/Mar/23

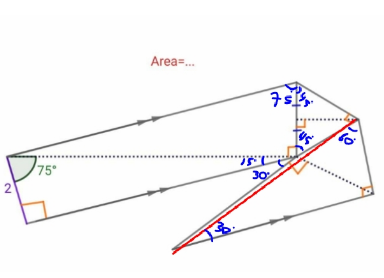
$${i}\:{think}\:{he}\:{meant}\:{this} \\ $$
Commented by HeferH last updated on 05/Mar/23
Answered by a.lgnaoui last updated on 04/Mar/23
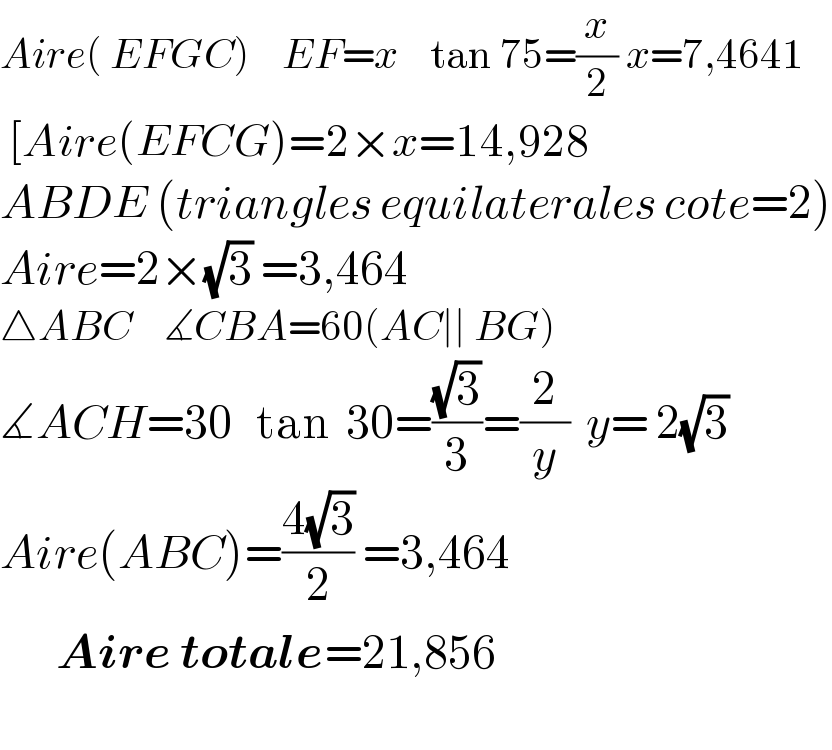
$${Aire}\left(\:{EFGC}\right)\:\:\:\:{EF}={x}\:\:\:\:\mathrm{tan}\:\mathrm{75}=\frac{{x}}{\mathrm{2}}\:{x}=\mathrm{7},\mathrm{4641} \\ $$$$\:\left[{Aire}\left({EFCG}\right)=\mathrm{2}×{x}=\mathrm{14},\mathrm{928}\right. \\ $$$${ABDE}\:\left({triangles}\:{equilaterales}\:{cote}=\mathrm{2}\right) \\ $$$${Aire}=\mathrm{2}×\sqrt{\mathrm{3}}\:=\mathrm{3},\mathrm{464} \\ $$$$\bigtriangleup{ABC}\:\:\:\:\measuredangle{CBA}=\mathrm{60}\left({AC}\mid\mid\:{BG}\right) \\ $$$$\measuredangle{ACH}=\mathrm{30}\:\:\:\mathrm{tan}\:\:\mathrm{30}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}=\frac{\mathrm{2}}{{y}}\:\:{y}=\:\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${Aire}\left({ABC}\right)=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{3},\mathrm{464} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{Aire}}\:\boldsymbol{{totale}}=\mathrm{21},\mathrm{856} \\ $$$$\:\:\: \\ $$
Commented by mr W last updated on 04/Mar/23
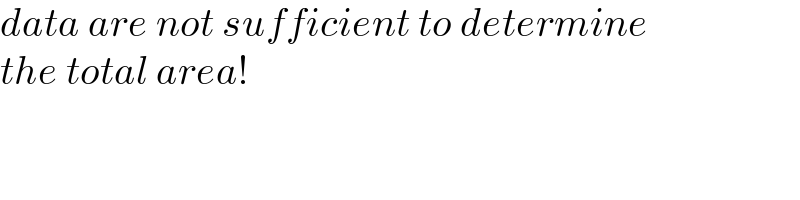
$${data}\:{are}\:{not}\:{sufficient}\:{to}\:{determine} \\ $$$${the}\:{total}\:{area}! \\ $$
Commented by a.lgnaoui last updated on 04/Mar/23
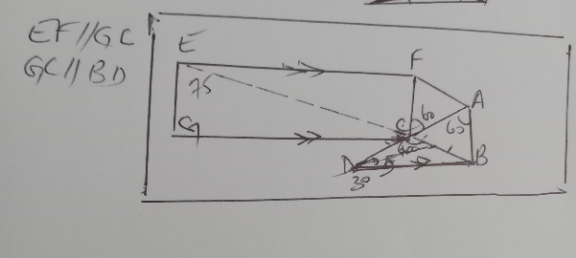
Commented by mr W last updated on 05/Mar/23
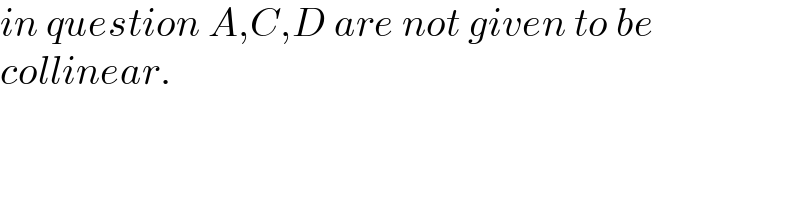
$${in}\:{question}\:{A},{C},{D}\:{are}\:{not}\:{given}\:{to}\:{be} \\ $$$${collinear}. \\ $$
