
Question Number 188621 by 073 last updated on 03/Mar/23

Answered by HeferH last updated on 04/Mar/23
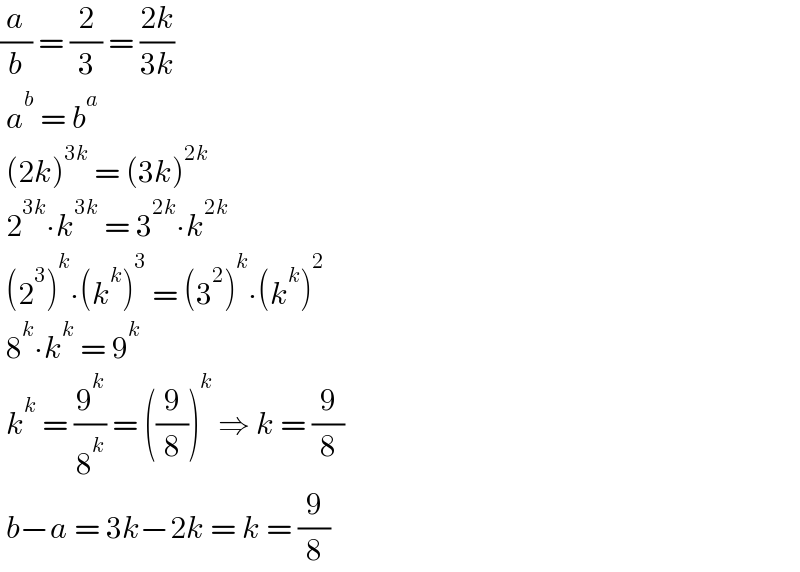
$$\frac{{a}}{{b}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:=\:\frac{\mathrm{2}{k}}{\mathrm{3}{k}} \\ $$$$\:{a}^{{b}} \:=\:{b}^{{a}} \\ $$$$\:\left(\mathrm{2}{k}\right)^{\mathrm{3}{k}} \:=\:\left(\mathrm{3}{k}\right)^{\mathrm{2}{k}} \\ $$$$\:\mathrm{2}^{\mathrm{3}{k}} \centerdot{k}^{\mathrm{3}{k}} \:=\:\mathrm{3}^{\mathrm{2}{k}} \centerdot{k}^{\mathrm{2}{k}} \\ $$$$\:\left(\mathrm{2}^{\mathrm{3}} \right)^{{k}} \centerdot\left({k}^{{k}} \right)^{\mathrm{3}} \:=\:\left(\mathrm{3}^{\mathrm{2}} \right)^{{k}} \centerdot\left({k}^{{k}} \right)^{\mathrm{2}} \\ $$$$\:\mathrm{8}^{{k}} \centerdot{k}^{{k}} \:=\:\mathrm{9}^{{k}} \\ $$$$\:{k}^{{k}} \:=\:\frac{\mathrm{9}^{{k}} }{\mathrm{8}^{{k}} }\:=\:\left(\frac{\mathrm{9}}{\mathrm{8}}\right)^{{k}} \:\Rightarrow\:{k}\:=\:\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\:{b}−{a}\:=\:\mathrm{3}{k}−\mathrm{2}{k}\:=\:{k}\:=\:\frac{\mathrm{9}}{\mathrm{8}} \\ $$
Commented by 073 last updated on 03/Mar/23

$$\mathrm{nice}\:\mathrm{solution} \\ $$
Answered by Frix last updated on 04/Mar/23
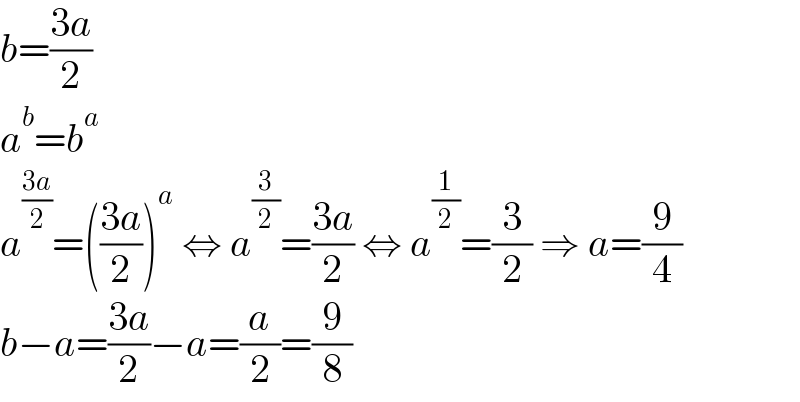
$${b}=\frac{\mathrm{3}{a}}{\mathrm{2}} \\ $$$${a}^{{b}} ={b}^{{a}} \\ $$$${a}^{\frac{\mathrm{3}{a}}{\mathrm{2}}} =\left(\frac{\mathrm{3}{a}}{\mathrm{2}}\right)^{{a}} \:\Leftrightarrow\:{a}^{\frac{\mathrm{3}}{\mathrm{2}}} =\frac{\mathrm{3}{a}}{\mathrm{2}}\:\Leftrightarrow\:{a}^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\:{a}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$${b}−{a}=\frac{\mathrm{3}{a}}{\mathrm{2}}−{a}=\frac{{a}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{8}} \\ $$
