
Question Number 115401 by Khalmohmmad last updated on 25/Sep/20

$$\int\frac{\sqrt{\mathrm{x}}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}=? \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20

$$\mathrm{2}\int\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt}=\int\frac{\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{i}\right)}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{i}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\mathrm{log}\left(\frac{\mathrm{t}−\sqrt{\mathrm{i}}}{\mathrm{t}+\sqrt{\mathrm{i}}}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{i}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{t}}{\:\sqrt{\mathrm{i}}} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 25/Sep/20
![Take limits ∫_0 ^∞ ((2t^2 )/(t^4 +1))=[(1/(2(√i)))log(((t−(√i))/(t+(√i))))]_0 ^∞ +[(1/( (√i)))tan^(−1) (t/( (√i)))]_0 ^∞ =lim_(t→∞) (1/(2(√i)))log(((1−((√i)/t))/(1+((√i)/t))))−(1/(2(√i)))log(−1)=(1/(2(√i)))log(−1) =0+(1/2)π(√i) (−log(−1)=log(−1)) And [(1/( (√i)))tan^(−1) (t/( (√i)))]_0 ^∞ =(π/(2(√i))) (π/2)((√i)+(1/( (√i))))=(π/2)(((i+1)/( (√i))))=(π/2)(((i+1)/(1+i)).(√2))=(π/( (√2))) (√i)=±((1+i)/( (√2))) Which is Real](Q115414.png)
$$\mathrm{Take}\:\mathrm{limits} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}=\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\mathrm{log}\left(\frac{\mathrm{t}−\sqrt{\mathrm{i}}}{\mathrm{t}+\sqrt{\mathrm{i}}}\right)\right]_{\mathrm{0}} ^{\infty} +\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{i}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{t}}{\:\sqrt{\mathrm{i}}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\underset{\mathrm{t}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\mathrm{log}\left(\frac{\mathrm{1}−\frac{\sqrt{\mathrm{i}}}{\mathrm{t}}}{\mathrm{1}+\frac{\sqrt{\mathrm{i}}}{\mathrm{t}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\mathrm{log}\left(−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{i}}}\mathrm{log}\left(−\mathrm{1}\right) \\ $$$$=\mathrm{0}+\frac{\mathrm{1}}{\mathrm{2}}\pi\sqrt{\mathrm{i}}\:\:\:\:\:\:\:\:\:\:\:\:\left(−\mathrm{log}\left(−\mathrm{1}\right)=\mathrm{log}\left(−\mathrm{1}\right)\right) \\ $$$$\mathrm{And} \\ $$$$\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{i}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{t}}{\:\sqrt{\mathrm{i}}}\right]_{\mathrm{0}} ^{\infty} =\frac{\pi}{\mathrm{2}\sqrt{\mathrm{i}}} \\ $$$$\frac{\pi}{\mathrm{2}}\left(\sqrt{\mathrm{i}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{i}}}\right)=\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{i}+\mathrm{1}}{\:\sqrt{\mathrm{i}}}\right)=\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{i}+\mathrm{1}}{\mathrm{1}+\mathrm{i}}.\sqrt{\mathrm{2}}\right)=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\:\:\:\:\:\:\sqrt{\mathrm{i}}=\pm\frac{\mathrm{1}+\mathrm{i}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{Which}\:\mathrm{is}\:\mathrm{Real} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Sep/20
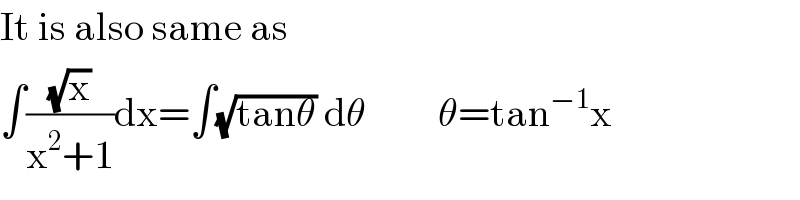
$$\mathrm{It}\:\mathrm{is}\:\mathrm{also}\:\mathrm{same}\:\mathrm{as} \\ $$$$\int\frac{\sqrt{\mathrm{x}}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}=\int\sqrt{\mathrm{tan}\theta}\:\mathrm{d}\theta\:\:\:\:\:\:\:\:\:\theta=\mathrm{tan}^{−\mathrm{1}} \mathrm{x} \\ $$
Answered by TANMAY PANACEA last updated on 25/Sep/20

$${x}={k}^{\mathrm{2}} \\ $$$$\int\frac{{k}}{{k}^{\mathrm{4}} +\mathrm{1}}×\mathrm{2}{kdk} \\ $$$$\int\frac{\mathrm{2}{dk}}{{k}^{\mathrm{2}} +\frac{\mathrm{1}}{{k}^{\mathrm{2}} }} \\ $$$$\int\frac{{d}\left({k}+\frac{\mathrm{1}}{{k}}\right)+{d}\left({k}−\frac{\mathrm{1}}{{k}}\right)}{{k}^{\mathrm{2}} +\frac{\mathrm{1}}{{k}^{\mathrm{2}} }} \\ $$$$\int\frac{{d}\left({k}+\frac{\mathrm{1}}{{k}}\right)}{\left({k}+\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} −\mathrm{2}}+\int\frac{{d}\left({k}−\frac{\mathrm{1}}{{k}}\right)}{\left({k}−\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} +\mathrm{2}} \\ $$$${now}\:{use}\:{formula}\:{pls} \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:{and}\:\int\frac{{dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} } \\ $$
