
Question Number 188492 by 073 last updated on 02/Mar/23
Commented by Rasheed.Sindhi last updated on 05/Mar/23
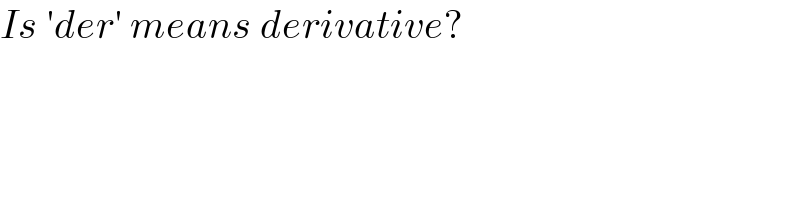
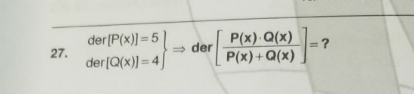
$${Is}\:'{der}'\:{means}\:{derivative}? \\ $$
Commented by 073 last updated on 06/Mar/23

$$\mathrm{der}\:\mathrm{is}\:\mathrm{degree}\:\mathrm{of}\:\mathrm{polynomal} \\ $$
Answered by Rasheed.Sindhi last updated on 05/Mar/23
![der[P(x)]=5⇒P(x)=5x+C der[Q(x)]=4⇒Q(x)=4x+C ((P(x)∙Q(x))/(P(x)+Q(x)))=(((5x+C)(4x+C))/((5x+C)+(4x+C))) =((20x^2 +C)/(9x+C)) der(((P(x)∙Q(x))/(P(x)+Q(x))))=der(((20x^2 +C)/(9x+C))) =(((9x)der(20x^2 )−(20x^2 )der(9x))/((9x)^2 )) =(((9x)(40x)−(20x^2 )(9))/(81x^2 )) =((360x^2 −180x^2 )/(81x^2 )) =((180x^2 )/(81x^2 ))=((20)/9)](Q188584.png)
$${der}\left[{P}\left({x}\right)\right]=\mathrm{5}\Rightarrow{P}\left({x}\right)=\mathrm{5}{x}+{C} \\ $$$${der}\left[{Q}\left({x}\right)\right]=\mathrm{4}\Rightarrow{Q}\left({x}\right)=\mathrm{4}{x}+{C} \\ $$$$\frac{{P}\left({x}\right)\centerdot{Q}\left({x}\right)}{{P}\left({x}\right)+{Q}\left({x}\right)}=\frac{\left(\mathrm{5}{x}+{C}\right)\left(\mathrm{4}{x}+{C}\right)}{\left(\mathrm{5}{x}+{C}\right)+\left(\mathrm{4}{x}+{C}\right)} \\ $$$$=\frac{\mathrm{20}{x}^{\mathrm{2}} +{C}}{\mathrm{9}{x}+{C}} \\ $$$${der}\left(\frac{{P}\left({x}\right)\centerdot{Q}\left({x}\right)}{{P}\left({x}\right)+{Q}\left({x}\right)}\right)={der}\left(\frac{\mathrm{20}{x}^{\mathrm{2}} +{C}}{\mathrm{9}{x}+{C}}\right) \\ $$$$=\frac{\left(\mathrm{9}{x}\right){der}\left(\mathrm{20}{x}^{\mathrm{2}} \right)−\left(\mathrm{20}{x}^{\mathrm{2}} \right){der}\left(\mathrm{9}{x}\right)}{\left(\mathrm{9}{x}\right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{9}{x}\right)\left(\mathrm{40}{x}\right)−\left(\mathrm{20}{x}^{\mathrm{2}} \right)\left(\mathrm{9}\right)}{\mathrm{81}{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{360}{x}^{\mathrm{2}} −\mathrm{180}{x}^{\mathrm{2}} }{\mathrm{81}{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{180}{x}^{\mathrm{2}} }{\mathrm{81}{x}^{\mathrm{2}} }=\frac{\mathrm{20}}{\mathrm{9}} \\ $$
Commented by Rasheed.Sindhi last updated on 05/Mar/23
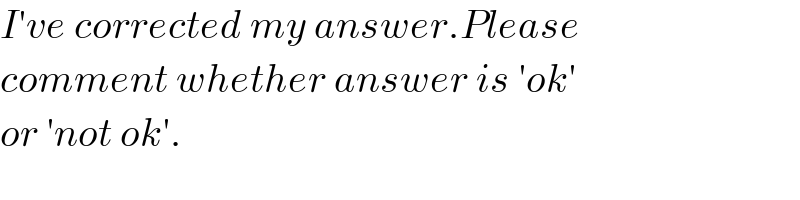
$${I}'{ve}\:{corrected}\:{my}\:{answer}.{Please} \\ $$$${comment}\:{whether}\:{answer}\:{is}\:'{ok}' \\ $$$${or}\:'{not}\:{ok}'. \\ $$
Commented by manxsol last updated on 05/Mar/23

$${C}_{\mathrm{1}\:\:\:\:\:{and}\:\:\:\:\:} {C}_{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:} \\ $$$${not}\:\:\:{C}\:\:\:\:\:{and}\:\:{C} \\ $$$$ \\ $$
Commented by 073 last updated on 06/Mar/23

$$\mathrm{no}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 06/Mar/23
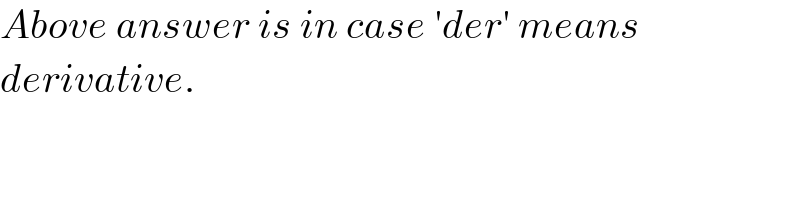
$${Above}\:{answer}\:{is}\:{in}\:{case}\:'{der}'\:{means} \\ $$$${derivative}. \\ $$
Commented by Rasheed.Sindhi last updated on 06/Mar/23
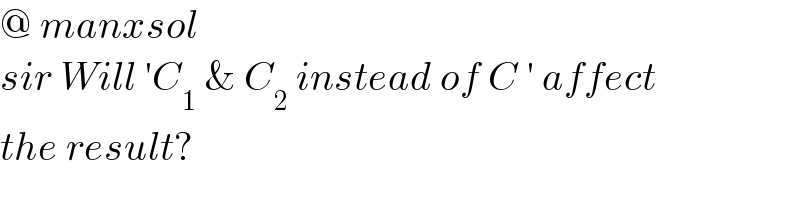
$$@\:{manxsol} \\ $$$${sir}\:{Will}\:'{C}_{\mathrm{1}} \:\&\:{C}_{\mathrm{2}} \:{instead}\:{of}\:{C}\:'\:{affect} \\ $$$${the}\:{result}? \\ $$
Commented by manxsol last updated on 06/Mar/23
![exercise initial is easy der(((x^5 .x^4 )/(x^5 +x^4 )))= der((x^9 /(x^5 +x^4 )))=9−5=4 you [((PQ)/(P+Q))]′= (((P+Q)[P ′Q+PQ′]−[P ′+Q ′)PQ)/((P+Q)^2 )) ((P^ P ′Q+P^2 Q′+Q^2 P′^() ′+QQ′P^() −PP′Q−P^() QQ′)/((P+Q)^2 ))(/) ((P^2 Q′+Q^2 P′)/((P+Q)^2 )) P=5x+C_1 Q=4x+C_2 (((5x+C_1 )^2 (4)+(4x+C_2 )^2 5)/((9x+C_1 +C_2 )^2 )) w ((180x^2 +40x(C_1 +C_2 )+4C_1 ^2 +5C_2 ^2 )/(81x^2 +18x(C_1 +C_2 )+(C_1 ^2 +C_2 ^2 ))) sir Will ′C_1 & C_2 instead of C ′ affect the result?](Q188740.png)
$${exercise}\:{initial}\:{is}\:{easy} \\ $$$${der}\left(\frac{{x}^{\mathrm{5}} .{x}^{\mathrm{4}} }{{x}^{\mathrm{5}} +{x}^{\mathrm{4}} }\right)= \\ $$$${der}\left(\frac{{x}^{\mathrm{9}} }{{x}^{\mathrm{5}} +{x}^{\mathrm{4}} }\right)=\mathrm{9}−\mathrm{5}=\mathrm{4} \\ $$$${you}\: \\ $$$$ \\ $$$$\left[\frac{{PQ}}{{P}+{Q}}\right]'= \\ $$$$\frac{\left({P}+{Q}\right)\left[{P}\:'{Q}+{PQ}'\right]−\left[{P}\:'+{Q}\:'\right){PQ}}{\left({P}+{Q}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\frac{\cancel{\overset{} {{P}P}\:'{Q}}+{P}^{\mathrm{2}} {Q}'+{Q}^{\mathrm{2}} \overset{} {{P}'}'+\cancel{\overset{} {{QQ}'{P}}}−\cancel{{PP}'{Q}}−\cancel{\overset{} {{P}QQ}}'}{\left({P}+{Q}\right)^{\mathrm{2}} }\frac{}{} \\ $$$$\frac{{P}^{\mathrm{2}} {Q}'+{Q}^{\mathrm{2}} {P}'}{\left({P}+{Q}\right)^{\mathrm{2}} } \\ $$$${P}=\mathrm{5}{x}+{C}_{\mathrm{1}} \\ $$$${Q}=\mathrm{4}{x}+{C}_{\mathrm{2}} \\ $$$$\frac{\left(\mathrm{5}{x}+{C}_{\mathrm{1}} \right)^{\mathrm{2}} \left(\mathrm{4}\right)+\left(\mathrm{4}{x}+{C}_{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{5}}{\left(\mathrm{9}{x}+{C}_{\mathrm{1}} +{C}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${w} \\ $$$$\frac{\mathrm{180}{x}^{\mathrm{2}} +\mathrm{40}{x}\left({C}_{\mathrm{1}} +{C}_{\mathrm{2}} \right)+\mathrm{4}{C}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{5}{C}_{\mathrm{2}} ^{\mathrm{2}} }{\mathrm{81}{x}^{\mathrm{2}} +\mathrm{18}{x}\left({C}_{\mathrm{1}} +{C}_{\mathrm{2}} \right)+\left({C}_{\mathrm{1}} ^{\mathrm{2}} +{C}_{\mathrm{2}} ^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$ \\ $$$${sir}\:{Will}\:'{C}_{\mathrm{1}} \:\&\:{C}_{\mathrm{2}} \:{instead}\:{of}\:{C}\:'\:{affect} \\ $$$${the}\:{result}? \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 06/Mar/23
![If ′der′ means degree of poly nomial._ der[P(x)]=5 , der[Q(x)]=4 der[((P(x)∙Q(x))/(P(x)+Q(x)))]=? Note that ((P(x)∙Q(x))/(P(x)+Q(x))) is polynomial if [P(x)+Q(x)] ∣ P(x)∙Q(x) Assuming above condition: •N=der[P(x).Q(x)]=der[P(x)]+der[Q(x)] =5+4=9 •D=der[P(x)+Q(x)]=max( der[P(x)]+der[Q(x)] ) =max(5,4)=5 •der[(N/D)]=der(N)−der(D) =9−5=4](Q188735.png)
$$\underline{{If}\:\:'{der}'\:{means}\:{degree}\:{of}\:\:{poly}\:{nomial}._{\:} } \\ $$$${der}\left[{P}\left({x}\right)\right]=\mathrm{5}\:,\:\:{der}\left[{Q}\left({x}\right)\right]=\mathrm{4} \\ $$$${der}\left[\frac{{P}\left({x}\right)\centerdot{Q}\left({x}\right)}{{P}\left({x}\right)+{Q}\left({x}\right)}\right]=? \\ $$$${Note}\:{that}\:\frac{{P}\left({x}\right)\centerdot{Q}\left({x}\right)}{{P}\left({x}\right)+{Q}\left({x}\right)}\:{is}\:{polynomial} \\ $$$${if}\:\left[{P}\left({x}\right)+{Q}\left({x}\right)\right]\:\mid\:{P}\left({x}\right)\centerdot{Q}\left({x}\right) \\ $$$${Assuming}\:{above}\:{condition}: \\ $$$$\bullet{N}={der}\left[{P}\left({x}\right).{Q}\left({x}\right)\right]={der}\left[{P}\left({x}\right)\right]+{der}\left[{Q}\left({x}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}+\mathrm{4}=\mathrm{9} \\ $$$$\bullet{D}={der}\left[{P}\left({x}\right)+{Q}\left({x}\right)\right]={max}\left(\:{der}\left[{P}\left({x}\right)\right]+{der}\left[{Q}\left({x}\right)\right]\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={max}\left(\mathrm{5},\mathrm{4}\right)=\mathrm{5} \\ $$$$\bullet{der}\left[\frac{{N}}{{D}}\right]={der}\left({N}\right)−{der}\left({D}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{9}−\mathrm{5}=\mathrm{4} \\ $$$$ \\ $$
Commented by 073 last updated on 06/Mar/23

$$\mathrm{nice}\:\mathrm{solution}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 06/Mar/23
$$\mathcal{T}{hank}\:{you}\:{for}\:{rapid}\:{response}. \\ $$
