
Question Number 188418 by 073 last updated on 01/Mar/23

Answered by manxsol last updated on 01/Mar/23
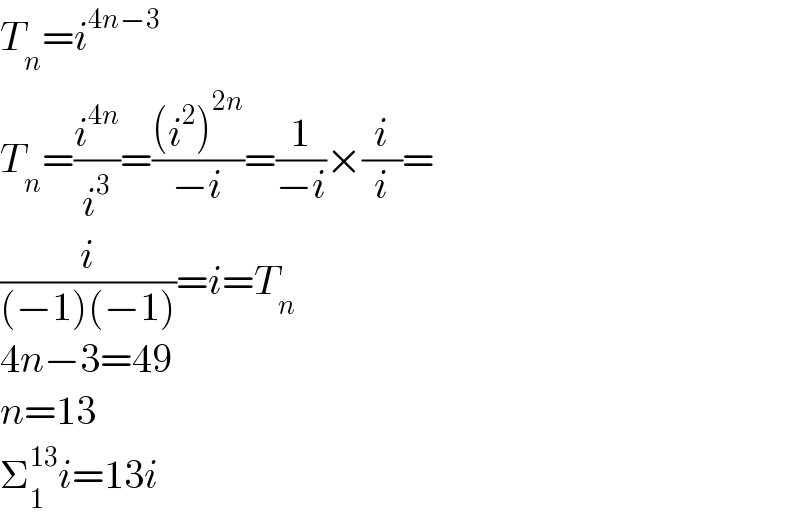
$${T}_{{n}} ={i}^{\mathrm{4}{n}−\mathrm{3}} \\ $$$${T}_{{n}} =\frac{{i}^{\mathrm{4}{n}} }{{i}^{\mathrm{3}} }=\frac{\left({i}^{\mathrm{2}} \right)^{\mathrm{2}{n}} }{−{i}}=\frac{\mathrm{1}}{−{i}}×\frac{{i}}{{i}}= \\ $$$$\frac{{i}}{\left(−\mathrm{1}\right)\left(−\mathrm{1}\right)}={i}={T}_{{n}} \\ $$$$\mathrm{4}{n}−\mathrm{3}=\mathrm{49} \\ $$$${n}=\mathrm{13} \\ $$$$\sum_{\mathrm{1}} ^{\mathrm{13}} {i}=\mathrm{13}{i} \\ $$
Answered by mehdee42 last updated on 01/Mar/23
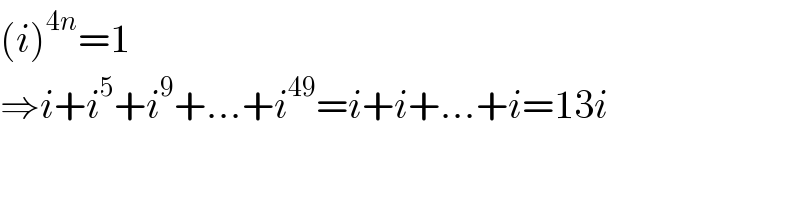
$$\left({i}\right)^{\mathrm{4}{n}} =\mathrm{1} \\ $$$$\Rightarrow{i}+{i}^{\mathrm{5}} +{i}^{\mathrm{9}} +...+{i}^{\mathrm{49}} ={i}+{i}+...+{i}=\mathrm{13}{i} \\ $$
