Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188262 by normans last updated on 27/Feb/23

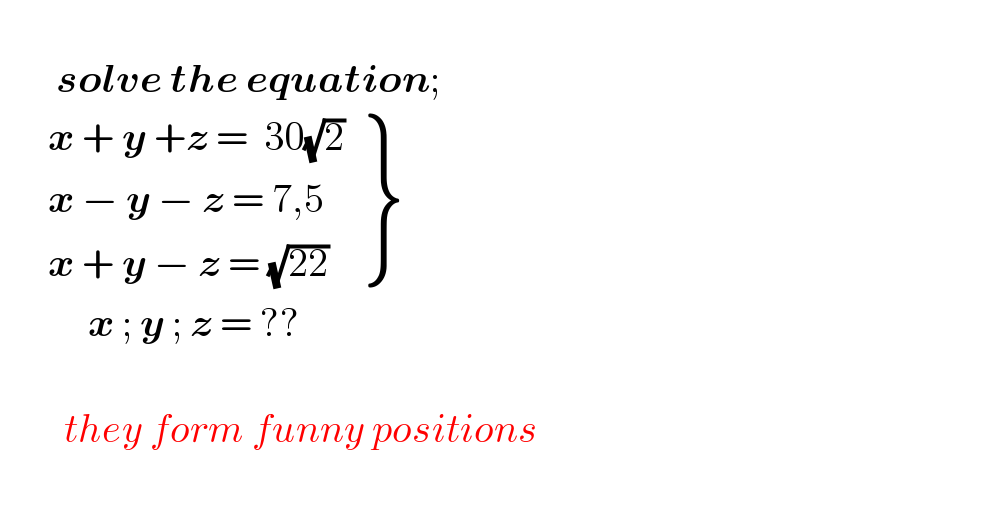
solve the equation; {: ((x + y +z = 30(√2))),((x − y − z = 7,5)),((x + y − z = (√(22)))) } x ; y ; z = ?? they form funny positions

$$ \\ $$$$\:\:\:\:\:\:\:\boldsymbol{{solve}}\:\boldsymbol{{the}}\:\boldsymbol{{equation}};\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\left.\begin{matrix}{\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:+\boldsymbol{{z}}\:=\:\:\mathrm{30}\sqrt{\mathrm{2}}}\\{\boldsymbol{{x}}\:−\:\boldsymbol{{y}}\:−\:\boldsymbol{{z}}\:=\:\mathrm{7},\mathrm{5}}\\{\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:−\:\boldsymbol{{z}}\:=\:\sqrt{\mathrm{22}}}\end{matrix}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{x}}\:;\:\boldsymbol{{y}}\:;\:\boldsymbol{{z}}\:=\:?? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:{they}\:{form}\:{funny}\:{positions}\: \\ $$$$ \\ $$

Answered by a.lgnaoui last updated on 27/Feb/23

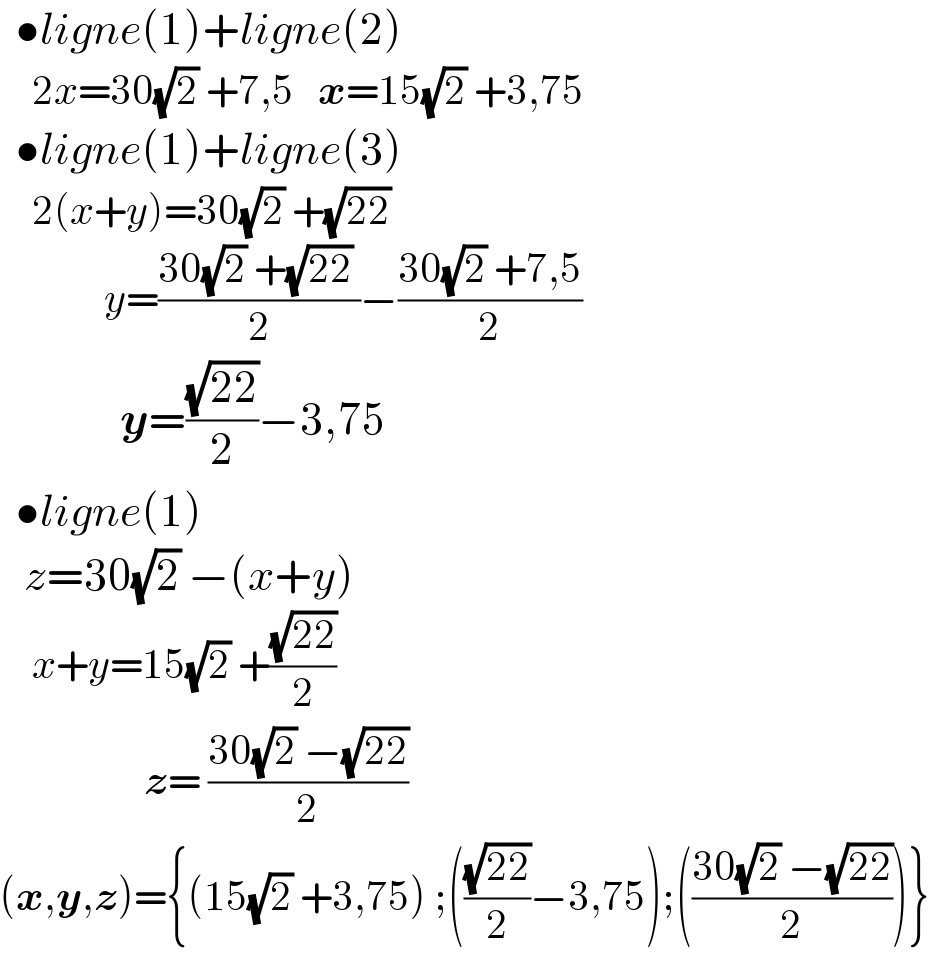
•ligne(1)+ligne(2) 2x=30(√2) +7,5 x=15(√2) +3,75 •ligne(1)+ligne(3) 2(x+y)=30(√2) +(√(22)) y=((30(√2) +(√(22)) )/2)−((30(√2) +7,5)/2) y=((√(22))/2)−3,75 •ligne(1) z=30(√2) −(x+y) x+y=15(√2) +((√(22))/2) z= ((30(√2) −(√(22)))/2) (x,y,z)={(15(√2) +3,75) ;(((√(22))/2)−3,75);(((30(√2) −(√(22)))/2))}

$$\:\:\bullet{ligne}\left(\mathrm{1}\right)+{ligne}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\mathrm{2}{x}=\mathrm{30}\sqrt{\mathrm{2}}\:+\mathrm{7},\mathrm{5}\:\:\:\boldsymbol{{x}}=\mathrm{15}\sqrt{\mathrm{2}}\:+\mathrm{3},\mathrm{75} \\ $$$$\:\:\bullet{ligne}\left(\mathrm{1}\right)+{ligne}\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\mathrm{2}\left({x}+{y}\right)=\mathrm{30}\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{22}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\frac{\mathrm{30}\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{22}}\:}{\mathrm{2}}−\frac{\mathrm{30}\sqrt{\mathrm{2}}\:+\mathrm{7},\mathrm{5}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{y}}=\frac{\sqrt{\mathrm{22}}}{\mathrm{2}}−\mathrm{3},\mathrm{75} \\ $$$$\:\:\bullet{ligne}\left(\mathrm{1}\right) \\ $$$$\:\:\:{z}=\mathrm{30}\sqrt{\mathrm{2}}\:−\left({x}+{y}\right) \\ $$$$\:\:\:\:{x}+{y}=\mathrm{15}\sqrt{\mathrm{2}}\:+\frac{\sqrt{\mathrm{22}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{z}}=\:\frac{\mathrm{30}\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{22}}}{\mathrm{2}} \\ $$$$\left(\boldsymbol{{x}},\boldsymbol{{y}},\boldsymbol{{z}}\right)=\left\{\left(\mathrm{15}\sqrt{\mathrm{2}}\:+\mathrm{3},\mathrm{75}\right)\:;\left(\frac{\sqrt{\mathrm{22}}}{\mathrm{2}}−\mathrm{3},\mathrm{75}\right);\left(\frac{\mathrm{30}\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{22}}}{\mathrm{2}}\right)\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com