Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 188196 by cortano12 last updated on 26/Feb/23

(1)solve Diopthantine equation 754x+221y=13 (2) find the number abcd such that 4×(abcd)=dcba

$$\left(\mathrm{1}\right)\mathrm{solve}\:\mathrm{Diopthantine}\:\mathrm{equation} \\ $$$$\:\:\:\:\:\mathrm{754x}+\mathrm{221y}=\mathrm{13} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{find}\:\mathrm{the}\:\mathrm{number}\:\mathrm{abcd}\: \\ $$$$\:\:\:\mathrm{such}\:\mathrm{that}\:\mathrm{4}×\left(\mathrm{abcd}\right)=\mathrm{dcba} \\ $$

Commented by ARUNG_Brandon_MBU last updated on 26/Feb/23

#include <iostream> using namespace std; int main(void) { for (int i=1000; i<2500; i++) { for(int j=1001; j<10000;j++) { if (4*i == j) if (i%10 == j/1000) if (i%100/10 == j%1000/100) if (i%1000/100 == j%100/10) if (i/1000 == j%10) cout << "4*" << i <<"=" << j; } } return 0; } // output: 4*2178=8712

Commented by ARUNG_Brandon_MBU last updated on 26/Feb/23

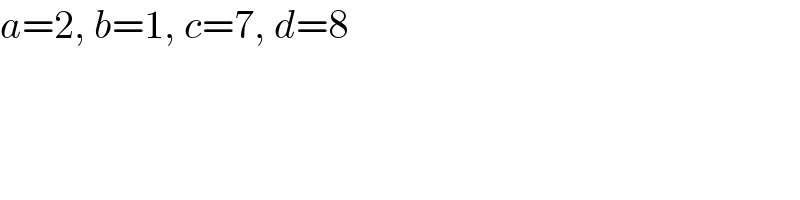
a=2, b=1, c=7, d=8

$${a}=\mathrm{2},\:{b}=\mathrm{1},\:{c}=\mathrm{7},\:{d}=\mathrm{8} \\ $$

Answered by ARUNG_Brandon_MBU last updated on 26/Feb/23

754x+221y=13 754=3(221)+91 221=2(91)+39 91=2(39)+13 ⇒13=91−2(39) =91−2[221−2(91)] =−2(221)+5(91) =−2(221)+5[754−3(221)] =5(754)−17(221) ⇒754(5)+221(−17)=13 ⇒x=5, y=−17

$$\mathrm{754}{x}+\mathrm{221y}=\mathrm{13} \\ $$$$\mathrm{754}=\mathrm{3}\left(\mathrm{221}\right)+\mathrm{91} \\ $$$$\mathrm{221}=\mathrm{2}\left(\mathrm{91}\right)+\mathrm{39} \\ $$$$\mathrm{91}=\mathrm{2}\left(\mathrm{39}\right)+\mathrm{13} \\ $$$$ \\ $$$$\Rightarrow\mathrm{13}=\mathrm{91}−\mathrm{2}\left(\mathrm{39}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{91}−\mathrm{2}\left[\mathrm{221}−\mathrm{2}\left(\mathrm{91}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\mathrm{2}\left(\mathrm{221}\right)+\mathrm{5}\left(\mathrm{91}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\mathrm{2}\left(\mathrm{221}\right)+\mathrm{5}\left[\mathrm{754}−\mathrm{3}\left(\mathrm{221}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{5}\left(\mathrm{754}\right)−\mathrm{17}\left(\mathrm{221}\right) \\ $$$$\Rightarrow\mathrm{754}\left(\mathrm{5}\right)+\mathrm{221}\left(−\mathrm{17}\right)=\mathrm{13} \\ $$$$\Rightarrow{x}=\mathrm{5},\:\mathrm{y}=−\mathrm{17} \\ $$

Answered by mr W last updated on 26/Feb/23

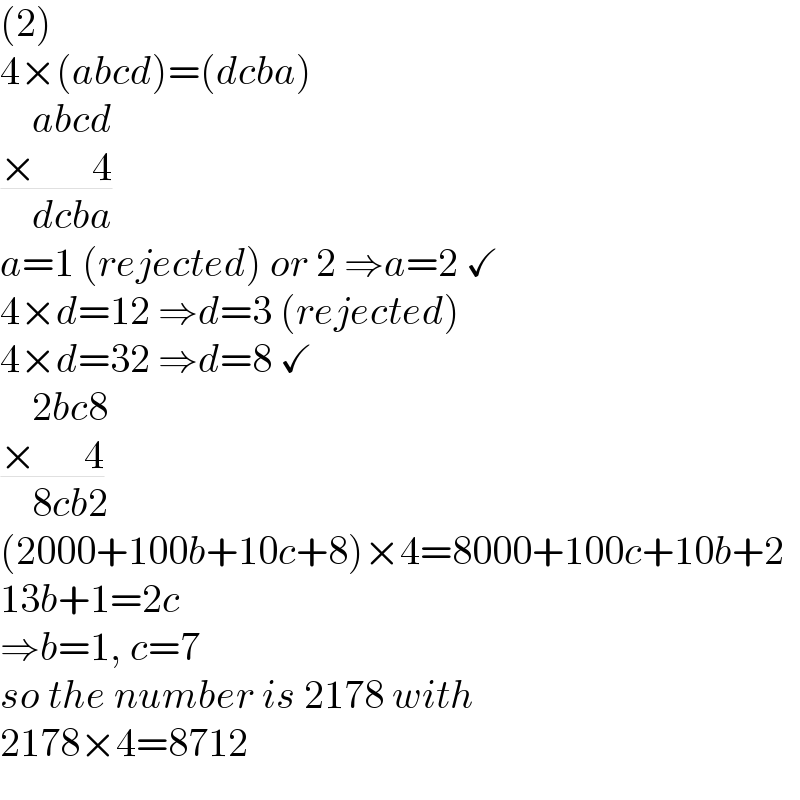
(2) 4×(abcd)=(dcba) abcd × 4 dcba a=1 (rejected) or 2 ⇒a=2 ✓ 4×d=12 ⇒d=3 (rejected) 4×d=32 ⇒d=8 ✓ 2bc8 × 4 8cb2 (2000+100b+10c+8)×4=8000+100c+10b+2 13b+1=2c ⇒b=1, c=7 so the number is 2178 with 2178×4=8712

$$\left(\mathrm{2}\right) \\ $$$$\mathrm{4}×\left({abcd}\right)=\left({dcba}\right) \\ $$$$\:\:\:\:{abcd} \\ $$$$\underline{×\:\:\:\:\:\:\:\mathrm{4}} \\ $$$$\:\:\:\:{dcba} \\ $$$${a}=\mathrm{1}\:\left({rejected}\right)\:{or}\:\mathrm{2}\:\Rightarrow{a}=\mathrm{2}\:\checkmark \\ $$$$\mathrm{4}×{d}=\mathrm{12}\:\Rightarrow{d}=\mathrm{3}\:\left({rejected}\right) \\ $$$$\mathrm{4}×{d}=\mathrm{32}\:\Rightarrow{d}=\mathrm{8}\:\checkmark \\ $$$$\:\:\:\:\mathrm{2}{bc}\mathrm{8} \\ $$$$\underline{×\:\:\:\:\:\:\mathrm{4}} \\ $$$$\:\:\:\:\mathrm{8}{cb}\mathrm{2} \\ $$$$\left(\mathrm{2000}+\mathrm{100}{b}+\mathrm{10}{c}+\mathrm{8}\right)×\mathrm{4}=\mathrm{8000}+\mathrm{100}{c}+\mathrm{10}{b}+\mathrm{2} \\ $$$$\mathrm{13}{b}+\mathrm{1}=\mathrm{2}{c} \\ $$$$\Rightarrow{b}=\mathrm{1},\:{c}=\mathrm{7} \\ $$$${so}\:{the}\:{number}\:{is}\:\mathrm{2178}\:{with} \\ $$$$\mathrm{2178}×\mathrm{4}=\mathrm{8712} \\ $$

Answered by manxsol last updated on 27/Feb/23

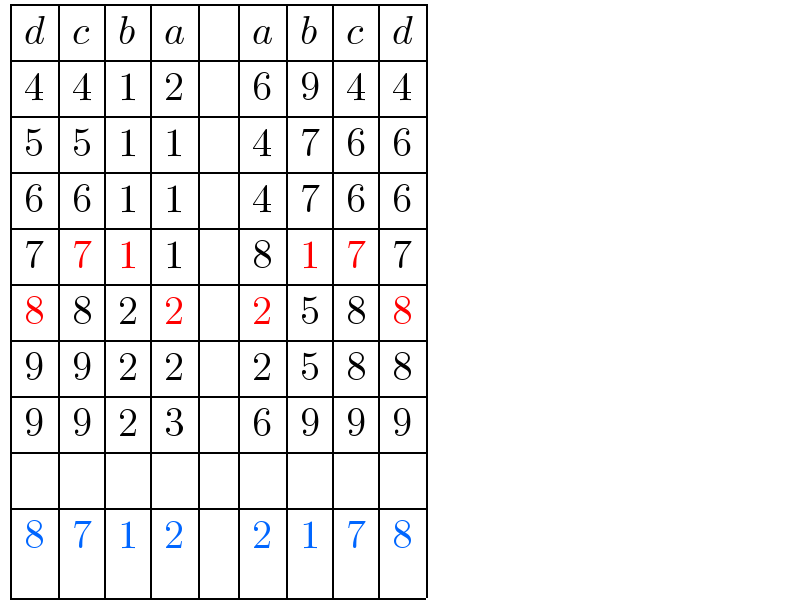
determinant ((d,c,b,a,,a,b,c,d),(4,4,1,2,,6,9,4,4),(5,5,1,1,,4,7,6,6),(6,6,1,1,,4,7,6,6),(7,7,1,1,,8,1,7,7),(8,8,2,2,,2,5,8,8),(9,9,2,2,,2,5,8,8),(9,9,2,3,,6,9,9,9),(,,,,,,,,),(8,7,1,2,,2,1,7,8))

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}{{d}}&\hline{{c}}&\hline{{b}}&\hline{{a}}&\hline{}&\hline{{a}}&\hline{{b}}&\hline{{c}}&\hline{{d}}\\{\mathrm{4}}&\hline{\mathrm{4}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{}&\hline{\mathrm{6}}&\hline{\mathrm{9}}&\hline{\mathrm{4}}&\hline{\mathrm{4}}\\{\mathrm{5}}&\hline{\mathrm{5}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{}&\hline{\mathrm{4}}&\hline{\mathrm{7}}&\hline{\mathrm{6}}&\hline{\mathrm{6}}\\{\mathrm{6}}&\hline{\mathrm{6}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{}&\hline{\mathrm{4}}&\hline{\mathrm{7}}&\hline{\mathrm{6}}&\hline{\mathrm{6}}\\{\mathrm{7}}&\hline{\mathrm{7}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{}&\hline{\mathrm{8}}&\hline{\mathrm{1}}&\hline{\mathrm{7}}&\hline{\mathrm{7}}\\{\mathrm{8}}&\hline{\mathrm{8}}&\hline{\mathrm{2}}&\hline{\mathrm{2}}&\hline{}&\hline{\mathrm{2}}&\hline{\mathrm{5}}&\hline{\mathrm{8}}&\hline{\mathrm{8}}\\{\mathrm{9}}&\hline{\mathrm{9}}&\hline{\mathrm{2}}&\hline{\mathrm{2}}&\hline{}&\hline{\mathrm{2}}&\hline{\mathrm{5}}&\hline{\mathrm{8}}&\hline{\mathrm{8}}\\{\mathrm{9}}&\hline{\mathrm{9}}&\hline{\mathrm{2}}&\hline{\mathrm{3}}&\hline{}&\hline{\mathrm{6}}&\hline{\mathrm{9}}&\hline{\mathrm{9}}&\hline{\mathrm{9}}\\{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}&\hline{}\\{\mathrm{8}}&\hline{\mathrm{7}}&\hline{\mathrm{1}}&\hline{\mathrm{2}}&\hline{}&\hline{\mathrm{2}}&\hline{\mathrm{1}}&\hline{\mathrm{7}}&\hline{\mathrm{8}}\\\hline\end{array} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com