Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 188177 by cortano12 last updated on 26/Feb/23

Commented by cortano12 last updated on 26/Feb/23

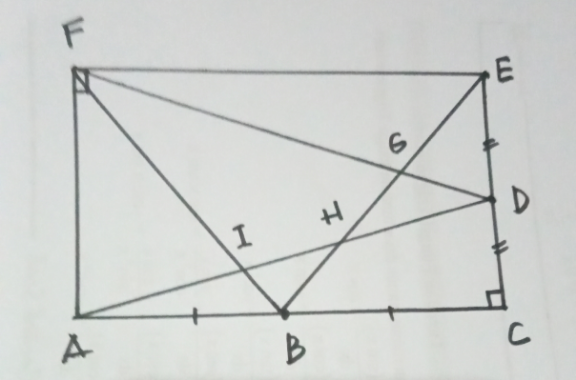
[ BCDH ] = 6m^2 [ ABI ] = 4m^2 [ DGE ] =2m^2 Find [ AIF ]

$$\:\left[\:\mathrm{BCDH}\:\right]\:=\:\mathrm{6m}^{\mathrm{2}} \\ $$$$\:\left[\:\mathrm{ABI}\:\right]\:=\:\mathrm{4m}^{\mathrm{2}} \\ $$$$\:\left[\:\mathrm{DGE}\:\right]\:=\mathrm{2m}^{\mathrm{2}} \\ $$$$\:\mathrm{Find}\:\left[\:\mathrm{AIF}\:\right] \\ $$

Commented by cortano12 last updated on 26/Feb/23

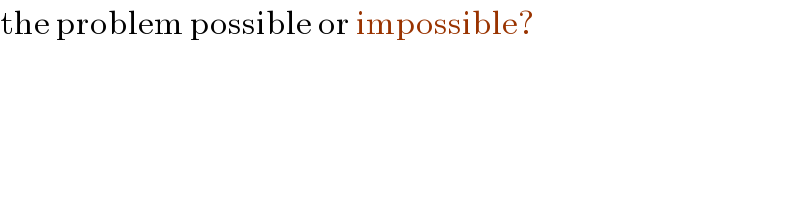
the problem possible or impossible?

$$\mathrm{the}\:\mathrm{problem}\:\mathrm{possible}\:\mathrm{or}\:\mathrm{impossible}? \\ $$

Answered by mr W last updated on 26/Feb/23

Commented by cortano12 last updated on 26/Feb/23

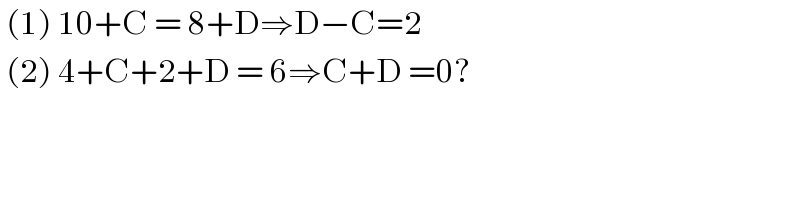
(1) 10+C = 8+D⇒D−C=2 (2) 4+C+2+D = 6⇒C+D =0?

$$\:\left(\mathrm{1}\right)\:\mathrm{10}+\mathrm{C}\:=\:\mathrm{8}+\mathrm{D}\Rightarrow\mathrm{D}−\mathrm{C}=\mathrm{2} \\ $$$$\:\left(\mathrm{2}\right)\:\mathrm{4}+\mathrm{C}+\mathrm{2}+\mathrm{D}\:=\:\mathrm{6}\Rightarrow\mathrm{C}+\mathrm{D}\:=\mathrm{0}? \\ $$

Commented by mr W last updated on 26/Feb/23

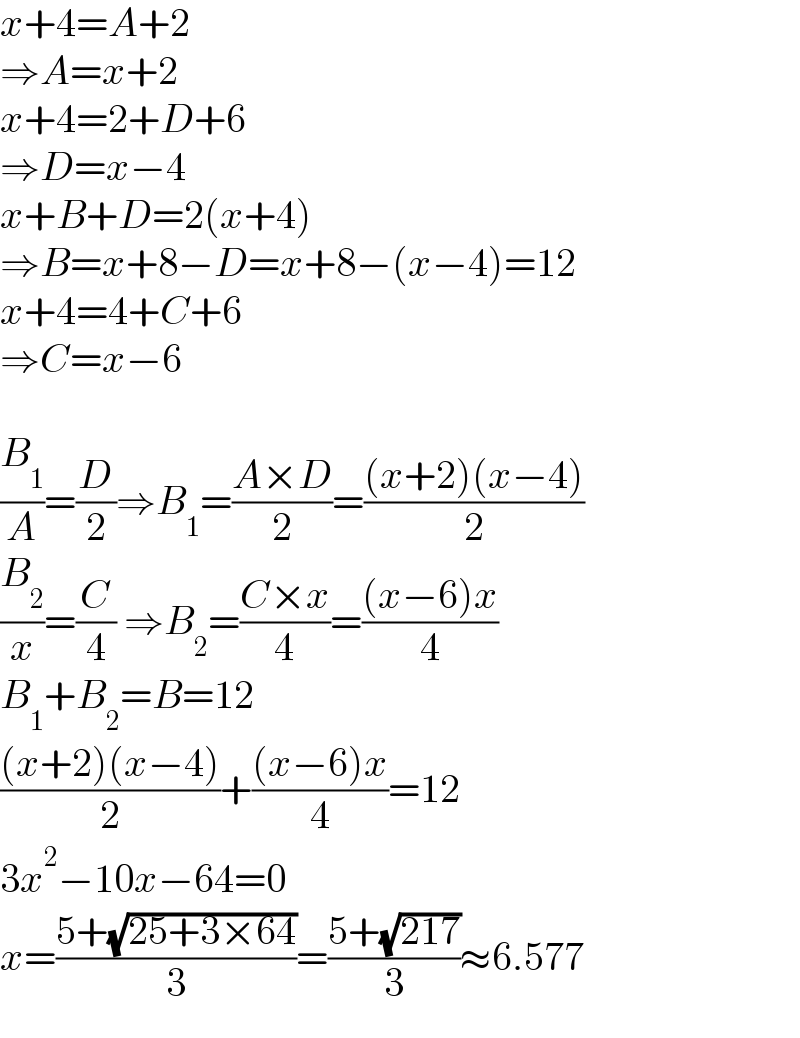
x+4=A+2 ⇒A=x+2 x+4=2+D+6 ⇒D=x−4 x+B+D=2(x+4) ⇒B=x+8−D=x+8−(x−4)=12 x+4=4+C+6 ⇒C=x−6 (B_1 /A)=(D/2)⇒B_1 =((A×D)/2)=(((x+2)(x−4))/2) (B_2 /x)=(C/4) ⇒B_2 =((C×x)/4)=(((x−6)x)/4) B_1 +B_2 =B=12 (((x+2)(x−4))/2)+(((x−6)x)/4)=12 3x^2 −10x−64=0 x=((5+(√(25+3×64)))/3)=((5+(√(217)))/3)≈6.577

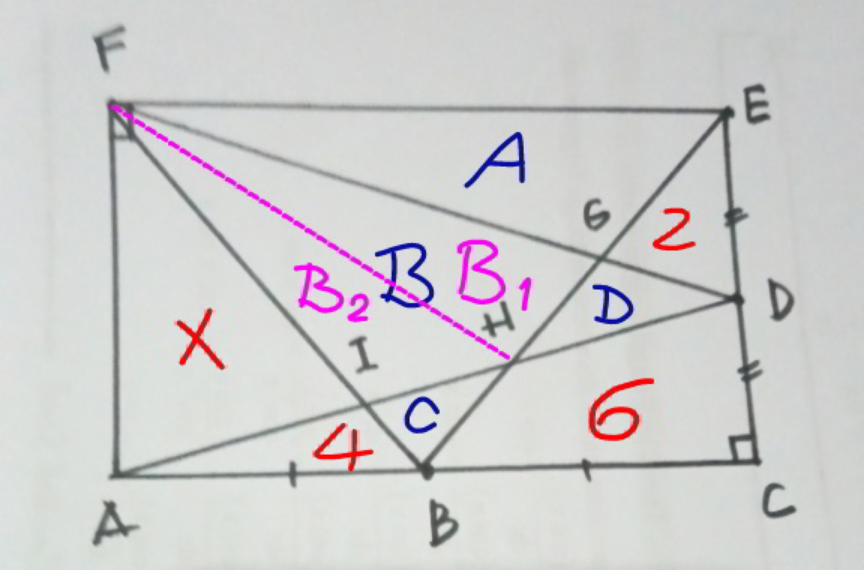
$${x}+\mathrm{4}={A}+\mathrm{2} \\ $$$$\Rightarrow{A}={x}+\mathrm{2} \\ $$$${x}+\mathrm{4}=\mathrm{2}+{D}+\mathrm{6} \\ $$$$\Rightarrow{D}={x}−\mathrm{4} \\ $$$${x}+{B}+{D}=\mathrm{2}\left({x}+\mathrm{4}\right) \\ $$$$\Rightarrow{B}={x}+\mathrm{8}−{D}={x}+\mathrm{8}−\left({x}−\mathrm{4}\right)=\mathrm{12} \\ $$$${x}+\mathrm{4}=\mathrm{4}+{C}+\mathrm{6} \\ $$$$\Rightarrow{C}={x}−\mathrm{6} \\ $$$$ \\ $$$$\frac{{B}_{\mathrm{1}} }{{A}}=\frac{{D}}{\mathrm{2}}\Rightarrow{B}_{\mathrm{1}} =\frac{{A}×{D}}{\mathrm{2}}=\frac{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{4}\right)}{\mathrm{2}} \\ $$$$\frac{{B}_{\mathrm{2}} }{{x}}=\frac{{C}}{\mathrm{4}}\:\Rightarrow{B}_{\mathrm{2}} =\frac{{C}×{x}}{\mathrm{4}}=\frac{\left({x}−\mathrm{6}\right){x}}{\mathrm{4}} \\ $$$${B}_{\mathrm{1}} +{B}_{\mathrm{2}} ={B}=\mathrm{12} \\ $$$$\frac{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{4}\right)}{\mathrm{2}}+\frac{\left({x}−\mathrm{6}\right){x}}{\mathrm{4}}=\mathrm{12} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{64}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{5}+\sqrt{\mathrm{25}+\mathrm{3}×\mathrm{64}}}{\mathrm{3}}=\frac{\mathrm{5}+\sqrt{\mathrm{217}}}{\mathrm{3}}\approx\mathrm{6}.\mathrm{577} \\ $$

Commented by cortano12 last updated on 26/Feb/23

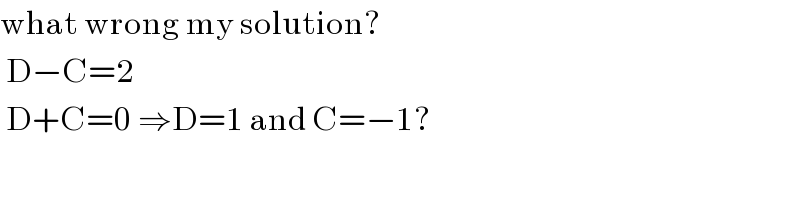
what wrong my solution? D−C=2 D+C=0 ⇒D=1 and C=−1?

$$\mathrm{what}\:\mathrm{wrong}\:\mathrm{my}\:\mathrm{solution}? \\ $$$$\:\mathrm{D}−\mathrm{C}=\mathrm{2} \\ $$$$\:\mathrm{D}+\mathrm{C}=\mathrm{0}\:\Rightarrow\mathrm{D}=\mathrm{1}\:\mathrm{and}\:\mathrm{C}=−\mathrm{1}? \\ $$

Commented by cortano12 last updated on 26/Feb/23

the answer x=7

$$\mathrm{the}\:\mathrm{answer}\:\mathrm{x}=\mathrm{7} \\ $$

Commented by cortano12 last updated on 26/Feb/23

Let [ BCH ] = u = 4+C let [ CDH ] = v= 2+D then u+v = 6 ⇒D+C =? i think impossible

$$\mathrm{Let}\:\left[\:\mathrm{BCH}\:\right]\:=\:\mathrm{u}\:=\:\mathrm{4}+\mathrm{C} \\ $$$$\:\mathrm{let}\:\left[\:\mathrm{CDH}\:\right]\:=\:\mathrm{v}=\:\mathrm{2}+\mathrm{D} \\ $$$$\:\mathrm{then}\:\mathrm{u}+\mathrm{v}\:=\:\mathrm{6}\:\Rightarrow\mathrm{D}+\mathrm{C}\:=? \\ $$$$\:\mathrm{i}\:\mathrm{think}\:\mathrm{impossible} \\ $$

Commented by mr W last updated on 26/Feb/23

we should select [ABI]+[DGE]≠[BCDH]

$${we}\:{should}\:{select}\:\left[{ABI}\right]+\left[{DGE}\right]\neq\left[{BCDH}\right] \\ $$

Commented by cortano12 last updated on 26/Feb/23

why?

$$\mathrm{why}? \\ $$

Commented by cortano12 last updated on 26/Feb/23

[ ABH ] = [ BCH ] , since AB=BC [ CDH ] = [ DHE ], since CD=DE so [ BCDH ] = [ BCH ]+ [ CHD ] 6 = 4+C + 2+D

$$\:\left[\:\mathrm{ABH}\:\right]\:=\:\left[\:\mathrm{BCH}\:\right]\:,\:\mathrm{since}\:\mathrm{AB}=\mathrm{BC} \\ $$$$\:\left[\:\mathrm{CDH}\:\right]\:=\:\left[\:\mathrm{DHE}\:\right],\:\mathrm{since}\:\mathrm{CD}=\mathrm{DE} \\ $$$$\:\mathrm{so}\:\left[\:\mathrm{BCDH}\:\right]\:=\:\left[\:\mathrm{BCH}\:\right]+\:\left[\:\mathrm{CHD}\:\right] \\ $$$$\:\mathrm{6}\:=\:\mathrm{4}+\mathrm{C}\:+\:\mathrm{2}+\mathrm{D} \\ $$

Commented by mr W last updated on 26/Feb/23

Commented by mr W last updated on 26/Feb/23

eqn. of AD: y=((xb)/(2a)) eqn. of BF: y=−((2b)/a)(x−(a/2)) eqn. of BE: y=((2b)/a)(x−(a/2)) eqn. of DF: y=b−((xb)/(2a)) intersection point I: y_I =((x_I b)/(2a))=−((2b)/a)(x_I −(a/2)) ⇒x_I =((2a)/5) ⇒y_I =(b/5) area X=(a/4)×(b/5)=((ab)/(20)) intersection point G: y_G =((2b)/a)(x_G −(a/2))=b−((x_G b)/(2a)) ⇒x_G =((4a)/5) ⇒y_G =((3b)/5) area Y=(b/4)×(a−((4a)/5))=((ab)/(20))=X intersection point H: y_H =((x_H b)/(2a))=((2b)/a)(x_H −(a/2)) ⇒x_H =((2a)/3) ⇒y_H =(b/3) area Z=(a/4)×(b/3)+(b/4)×(a−((2a)/3))=((ab)/6)>X+Y we see: area X=area Y area Z≠area X+area Y

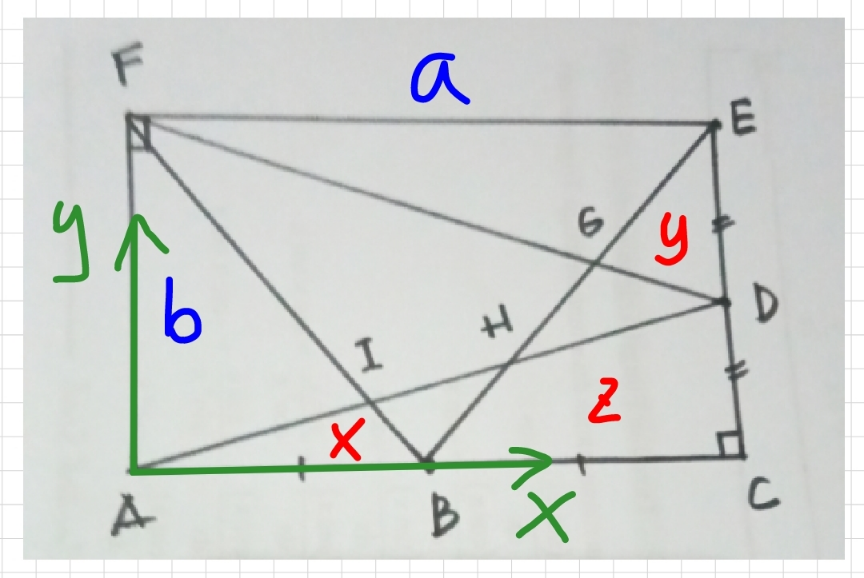
$${eqn}.\:{of}\:{AD}: \\ $$$${y}=\frac{{xb}}{\mathrm{2}{a}} \\ $$$${eqn}.\:{of}\:{BF}: \\ $$$${y}=−\frac{\mathrm{2}{b}}{{a}}\left({x}−\frac{{a}}{\mathrm{2}}\right) \\ $$$${eqn}.\:{of}\:{BE}: \\ $$$${y}=\frac{\mathrm{2}{b}}{{a}}\left({x}−\frac{{a}}{\mathrm{2}}\right) \\ $$$${eqn}.\:{of}\:{DF}: \\ $$$${y}={b}−\frac{{xb}}{\mathrm{2}{a}} \\ $$$${intersection}\:{point}\:{I}: \\ $$$${y}_{{I}} =\frac{{x}_{{I}} {b}}{\mathrm{2}{a}}=−\frac{\mathrm{2}{b}}{{a}}\left({x}_{{I}} −\frac{{a}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}_{{I}} =\frac{\mathrm{2}{a}}{\mathrm{5}} \\ $$$$\Rightarrow{y}_{{I}} =\frac{{b}}{\mathrm{5}} \\ $$$${area}\:{X}=\frac{{a}}{\mathrm{4}}×\frac{{b}}{\mathrm{5}}=\frac{{ab}}{\mathrm{20}} \\ $$$${intersection}\:{point}\:{G}: \\ $$$${y}_{{G}} =\frac{\mathrm{2}{b}}{{a}}\left({x}_{{G}} −\frac{{a}}{\mathrm{2}}\right)={b}−\frac{{x}_{{G}} {b}}{\mathrm{2}{a}} \\ $$$$\Rightarrow{x}_{{G}} =\frac{\mathrm{4}{a}}{\mathrm{5}} \\ $$$$\Rightarrow{y}_{{G}} =\frac{\mathrm{3}{b}}{\mathrm{5}} \\ $$$${area}\:{Y}=\frac{{b}}{\mathrm{4}}×\left({a}−\frac{\mathrm{4}{a}}{\mathrm{5}}\right)=\frac{{ab}}{\mathrm{20}}={X} \\ $$$${intersection}\:{point}\:{H}: \\ $$$${y}_{{H}} =\frac{{x}_{{H}} {b}}{\mathrm{2}{a}}=\frac{\mathrm{2}{b}}{{a}}\left({x}_{{H}} −\frac{{a}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}_{{H}} =\frac{\mathrm{2}{a}}{\mathrm{3}} \\ $$$$\Rightarrow{y}_{{H}} =\frac{{b}}{\mathrm{3}} \\ $$$${area}\:{Z}=\frac{{a}}{\mathrm{4}}×\frac{{b}}{\mathrm{3}}+\frac{{b}}{\mathrm{4}}×\left({a}−\frac{\mathrm{2}{a}}{\mathrm{3}}\right)=\frac{{ab}}{\mathrm{6}}>{X}+{Y} \\ $$$${we}\:{see}: \\ $$$${area}\:{X}={area}\:{Y} \\ $$$${area}\:{Z}\neq{area}\:{X}+{area}\:{Y} \\ $$

Commented by mr W last updated on 26/Feb/23

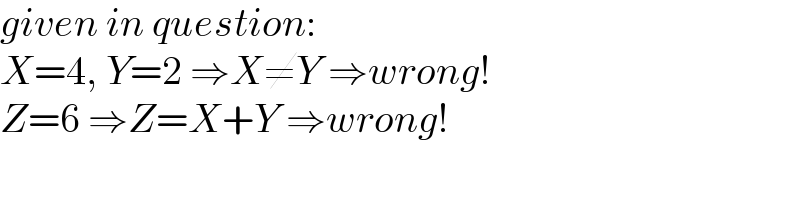
given in question: X=4, Y=2 ⇒X≠Y ⇒wrong! Z=6 ⇒Z=X+Y ⇒wrong!

$${given}\:{in}\:{question}: \\ $$$${X}=\mathrm{4},\:{Y}=\mathrm{2}\:\Rightarrow{X}\neq{Y}\:\Rightarrow{wrong}! \\ $$$${Z}=\mathrm{6}\:\Rightarrow{Z}={X}+{Y}\:\Rightarrow{wrong}! \\ $$

Commented by mr W last updated on 26/Feb/23

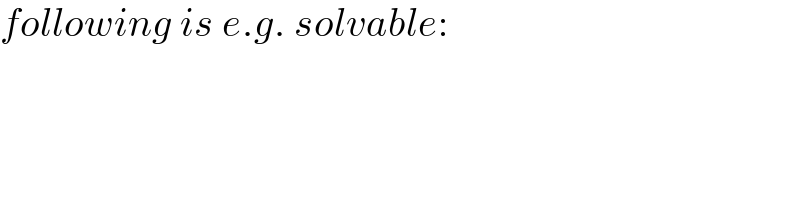
following is e.g. solvable:

$${following}\:{is}\:{e}.{g}.\:{solvable}: \\ $$

Commented by mr W last updated on 26/Feb/23

Answered by horsebrand11 last updated on 26/Feb/23

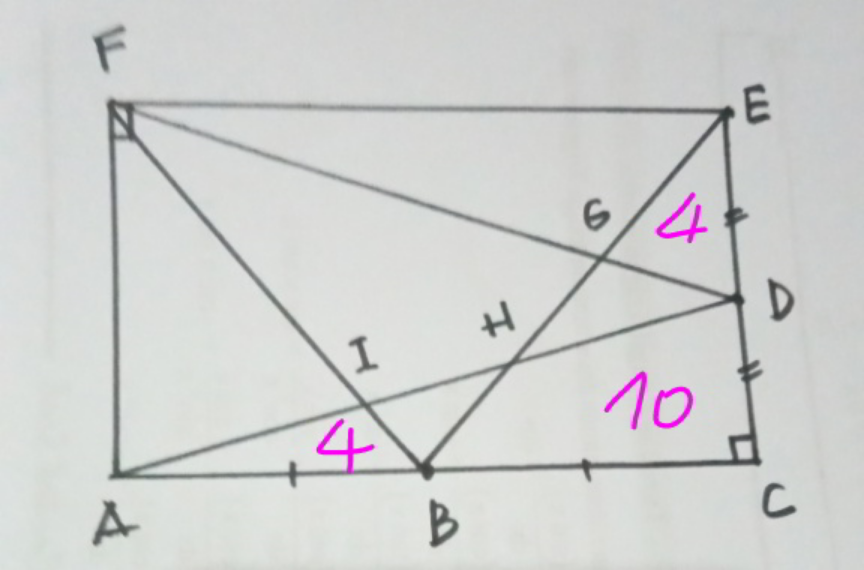
it should be [ BCHD ]=10 ⇒4+C+2+D=10; C+D=4 ⇒14+C=12+D⇒D−C=2 then { ((D=3)),((C=1)) :} , it clear [ AFI ]= 11

$${it}\:{should}\:{be}\:\left[\:{BCHD}\:\right]=\mathrm{10} \\ $$$$\Rightarrow\mathrm{4}+{C}+\mathrm{2}+{D}=\mathrm{10};\:{C}+{D}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{14}+{C}=\mathrm{12}+{D}\Rightarrow{D}−{C}=\mathrm{2} \\ $$$${then}\:\begin{cases}{{D}=\mathrm{3}}\\{{C}=\mathrm{1}}\end{cases}\:,\:{it}\:{clear}\:\left[\:{AFI}\:\right]=\:\mathrm{11} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com