
Question Number 188164 by cortano12 last updated on 26/Feb/23
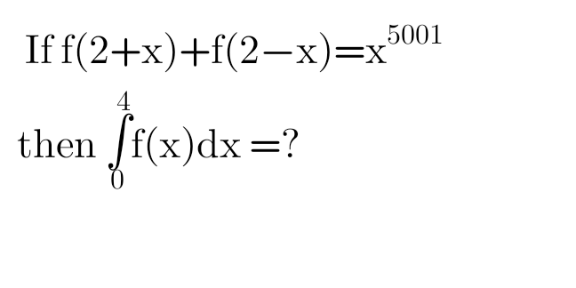
Commented by cortano12 last updated on 01/Mar/23
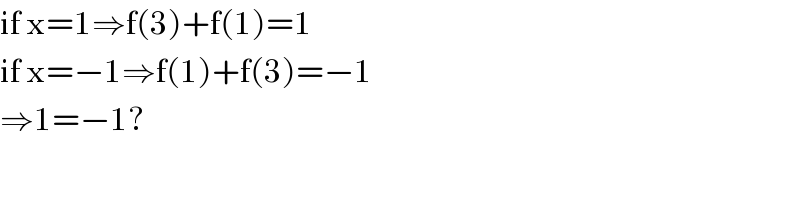
$$\mathrm{if}\:\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{f}\left(\mathrm{3}\right)+\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{if}\:\mathrm{x}=−\mathrm{1}\Rightarrow\mathrm{f}\left(\mathrm{1}\right)+\mathrm{f}\left(\mathrm{3}\right)=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}=−\mathrm{1}?\: \\ $$
Answered by mr W last updated on 26/Feb/23
![∫_0 ^4 f(x)dx =∫_0 ^2 f(x)dx+∫_2 ^4 f(x)dx =∫_(−2) ^0 f(t+2)dt−∫_0 ^(−2) f(2−t)dt =∫_(−2) ^0 f(t+2)dt+∫_(−2) ^0 f(2−t)dt =∫_(−2) ^0 [f(t+2)+f(2−t)]dt =∫_(−2) ^0 t^(5001) d(t) =[(t^(5002) /(5002))]_(−2) ^0 =−(2^(5002) /(5002))](Q188176.png)
$$\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} {f}\left({x}\right){dx}+\int_{\mathrm{2}} ^{\mathrm{4}} {f}\left({x}\right){dx} \\ $$$$=\int_{−\mathrm{2}} ^{\mathrm{0}} {f}\left({t}+\mathrm{2}\right){dt}−\int_{\mathrm{0}} ^{−\mathrm{2}} {f}\left(\mathrm{2}−{t}\right){dt} \\ $$$$=\int_{−\mathrm{2}} ^{\mathrm{0}} {f}\left({t}+\mathrm{2}\right){dt}+\int_{−\mathrm{2}} ^{\mathrm{0}} {f}\left(\mathrm{2}−{t}\right){dt} \\ $$$$=\int_{−\mathrm{2}} ^{\mathrm{0}} \left[{f}\left({t}+\mathrm{2}\right)+{f}\left(\mathrm{2}−{t}\right)\right]{dt} \\ $$$$=\int_{−\mathrm{2}} ^{\mathrm{0}} {t}^{\mathrm{5001}} {d}\left({t}\right) \\ $$$$=\left[\frac{{t}^{\mathrm{5002}} }{\mathrm{5002}}\right]_{−\mathrm{2}} ^{\mathrm{0}} \\ $$$$=−\frac{\mathrm{2}^{\mathrm{5002}} }{\mathrm{5002}} \\ $$
Commented by cortano12 last updated on 26/Feb/23

$$\mathrm{yes}\:\mathrm{nice} \\ $$
Commented by cortano12 last updated on 01/Mar/23
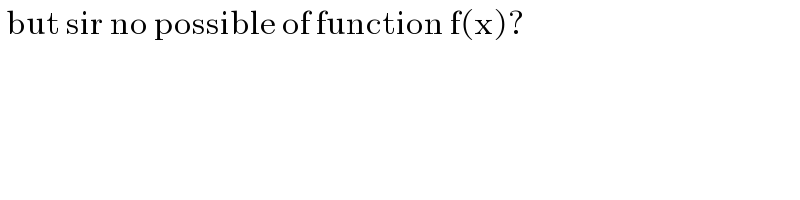
$$\:\mathrm{but}\:\mathrm{sir}\:\mathrm{no}\:\mathrm{possible}\:\mathrm{of}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)?\: \\ $$
