
Question Number 188107 by pascal889 last updated on 25/Feb/23
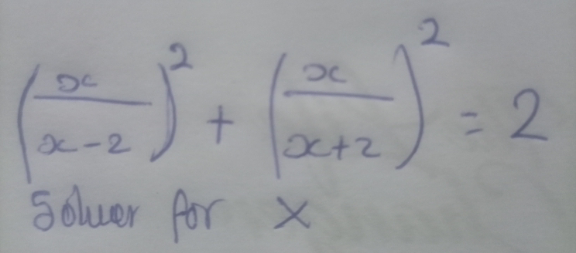
Answered by CElcedricjunior last updated on 25/Feb/23

$$\left(\frac{\boldsymbol{{x}}}{\boldsymbol{{x}}−\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\boldsymbol{{x}}}{\boldsymbol{{x}}+\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{2}\: \\ $$$$\exists\boldsymbol{{ssi}}\:\boldsymbol{{x}}\neq−\mathrm{2}\:\boldsymbol{{et}}\:\boldsymbol{{x}}\neq\mathrm{2} \\ $$$$=>\boldsymbol{{x}}^{\mathrm{2}} \left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{{x}}+\mathrm{4}\right)+\boldsymbol{{x}}^{\mathrm{2}} \left(\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)=\mathrm{2}\left(\boldsymbol{{x}}^{\mathrm{4}} −\mathrm{8}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{16}\right)\bigstar{Moivre} \\ $$$$=>\mathrm{8}\boldsymbol{{x}}^{\mathrm{2}} =\mathrm{32}−\mathrm{16}\boldsymbol{{x}}^{\mathrm{2}} \bigstar\mathscr{C}{edric}\:{junior} \\ $$$$=>\mathrm{24}\boldsymbol{{x}}^{\mathrm{2}} =\mathrm{32}=>\boldsymbol{{x}}=\mp\sqrt{\frac{\mathrm{4}}{\mathrm{3}}}=\mp\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$${S}_{\mathbb{R}} =\left\{−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}};\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\right\} \\ $$$$ \\ $$
Answered by otchereabdullai last updated on 25/Feb/23
![((x/(x−2)))((x/(x−2)))+((x/(x+2)))((x/(x+2)))=2 (x^2 /(x(x−2)−2(x−2))) + (x^2 /(x(x+2)+2(x+2)))=2 (x^2 /(x^2 −2x−2x+4)) + (x^2 /(x^2 +2x+2x+4))=2 (x^2 /(x^2 −4x+4)) + (x^2 /(x^2 +4x+4))=2 lcm=(x^2 −4x+4)(x^2 +4x+4) multiply through by the lcm we have x^2 (x^2 +4x+4)+x^2 (x^2 −4x+4)=2[(x^2 −4x+4)(x^2 +4x+4)] expand and cancil opposite like terms we have −32x^2 +8x+32=0 −24x^2 +32=0 −24x^2 =−32 24x^2 =32 x^2 =((32)/(24)) x=±(√((32)/(24))) x=±((4(√2))/(2(√6))) x=±((2(√3))/3)](Q188113.png)
$$\:\:\:\left(\frac{{x}}{{x}−\mathrm{2}}\right)\left(\frac{{x}}{{x}−\mathrm{2}}\right)+\left(\frac{{x}}{{x}+\mathrm{2}}\right)\left(\frac{{x}}{{x}+\mathrm{2}}\right)=\mathrm{2} \\ $$$$\:\frac{{x}^{\mathrm{2}} }{{x}\left({x}−\mathrm{2}\right)−\mathrm{2}\left({x}−\mathrm{2}\right)}\:+\:\frac{{x}^{\mathrm{2}} }{{x}\left({x}+\mathrm{2}\right)+\mathrm{2}\left({x}+\mathrm{2}\right)}=\mathrm{2} \\ $$$$\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{2}{x}+\mathrm{4}}\:+\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}{x}+\mathrm{4}}=\mathrm{2} \\ $$$$\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}}\:+\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}=\mathrm{2} \\ $$$$\:{lcm}=\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}\right) \\ $$$${multiply}\:{through}\:{by}\:{the}\:{lcm}\:{we}\:{have} \\ $$$${x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}\right)+{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)=\mathrm{2}\left[\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}\right)\right] \\ $$$${expand}\:{and}\:{cancil}\:{opposite}\:{like}\:{terms} \\ $$$${we}\:{have}\:−\mathrm{32}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{32}=\mathrm{0} \\ $$$$\:\:−\mathrm{24}{x}^{\mathrm{2}} +\mathrm{32}=\mathrm{0} \\ $$$$\:\:−\mathrm{24}{x}^{\mathrm{2}} =−\mathrm{32} \\ $$$$\:\:\:\mathrm{24}{x}^{\mathrm{2}} =\mathrm{32} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\frac{\mathrm{32}}{\mathrm{24}} \\ $$$$\:\:\:\:\:\:\:\:{x}=\pm\sqrt{\frac{\mathrm{32}}{\mathrm{24}}} \\ $$$$\:\:\:\:\:\:\:\:\:{x}=\pm\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{6}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}=\pm\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$ \\ $$
