
Question Number 188086 by universe last updated on 25/Feb/23
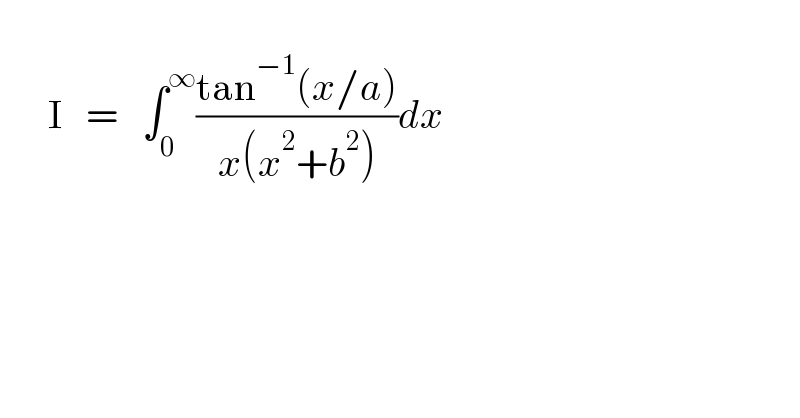
$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\mathrm{I}\:\:\:=\:\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \left({x}/{a}\right)}{{x}\left({x}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{dx} \\ $$
Answered by witcher3 last updated on 25/Feb/23

$$\mathrm{for}\:\mathrm{a}>\mathrm{0} \\ $$$$\frac{\mathrm{x}}{\mathrm{a}}=\mathrm{y} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{y}\right)}{\mathrm{y}\left(\mathrm{a}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}\mathrm{dy} \\ $$$$\frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{y}\right)}{\mathrm{y}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} } \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dydz}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \right)} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dy}}{\left(\mathrm{a}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \right)}=\mathrm{2i}\pi.\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2aib}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \mathrm{z}^{\mathrm{2}} \right)} \\ $$$$+\mathrm{2i}\pi.\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{2iz}\left(\mathrm{b}^{\mathrm{2}} \mathrm{z}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)} \\ $$$$=\frac{\pi\mathrm{a}}{\mathrm{b}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \mathrm{z}^{\mathrm{2}} \right)}+\frac{\pi\mathrm{z}}{\left(\mathrm{b}^{\mathrm{2}} \mathrm{z}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)}=\pi\left(\frac{\mathrm{z}−\frac{\mathrm{a}}{\mathrm{b}}}{\left(\mathrm{bz}−\mathrm{a}\right)\left(\mathrm{bz}+\mathrm{a}\right)}\right) \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\pi}{\mathrm{b}\left(\mathrm{bz}+\mathrm{a}\right)}=\frac{\pi}{\mathrm{b}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{a}}{\mathrm{b}}\right) \\ $$
