
Question Number 188037 by Michaelfaraday last updated on 25/Feb/23

$${find}\:\frac{{dy}}{{dx}} \\ $$$${y}=\mathrm{2}{x}^{\sqrt{{x}}} \\ $$
Answered by horsebrand11 last updated on 25/Feb/23
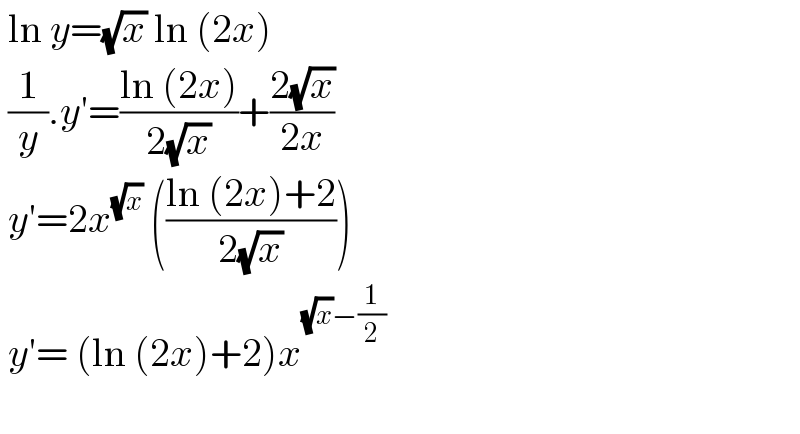
$$\:\mathrm{ln}\:{y}=\sqrt{{x}}\:\mathrm{ln}\:\left(\mathrm{2}{x}\right) \\ $$$$\:\frac{\mathrm{1}}{{y}}.{y}'=\frac{\mathrm{ln}\:\left(\mathrm{2}{x}\right)}{\mathrm{2}\sqrt{{x}}}+\frac{\mathrm{2}\sqrt{{x}}}{\mathrm{2}{x}} \\ $$$$\:{y}'=\mathrm{2}{x}^{\sqrt{{x}}} \:\left(\frac{\mathrm{ln}\:\left(\mathrm{2}{x}\right)+\mathrm{2}}{\mathrm{2}\sqrt{{x}}}\right) \\ $$$$\:{y}'=\:\left(\mathrm{ln}\:\left(\mathrm{2}{x}\right)+\mathrm{2}\right){x}^{\sqrt{{x}}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$ \\ $$
Commented by Michaelfaraday last updated on 25/Feb/23

$${thanks}\:{sir} \\ $$
