
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 187948 by horsebrand11 last updated on 24/Feb/23

$$ \\ $$$$\mathrm{Given}\:\mathrm{a}\:\mathrm{set}\:\mathrm{H}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{300}.\:\mathrm{We}\:\mathrm{will}\:\mathrm{a}\right. \\ $$$$\mathrm{cre}{a}\mathrm{te}\:\mathrm{a}\:\mathrm{subset}\:\mathrm{of}\:\mathrm{H}\:\mathrm{consisting}\:\mathrm{of}\: \\ $$$$\mathrm{thre}{e}\:\mathrm{elements}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{thr}{e}\mathrm{e}\:\mathrm{elements}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3}\:\: \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{subsets}\:\mathrm{that}\: \\ $$$$\mathrm{canbe}\:\mathrm{made}\:\mathrm{is}\:\mathrm{x}.\:\mathrm{Find}\:\mathrm{the} \\ $$$$\mathrm{remaind}{e}\mathrm{r}\:\mathrm{if}\:\mathrm{x}\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{100000} \\ $$
Answered by mr W last updated on 24/Feb/23

$${H}_{\mathrm{1}} =\left\{\mathrm{1},\mathrm{4},\mathrm{7},..,\mathrm{298}\right\}\:{with}\:\mathrm{100}\:{elements} \\ $$$${H}_{\mathrm{2}} =\left\{\mathrm{2},\mathrm{5},\mathrm{8},..,\mathrm{299}\right\}\:{with}\:\mathrm{100}\:{elements} \\ $$$${H}_{\mathrm{3}} =\left\{\mathrm{3},\mathrm{6},\mathrm{9},..,\mathrm{300}\right\}\:{with}\:\mathrm{100}\:{elements} \\ $$$${such}\:{that}\:{the}\:{sum}\:{of}\:\mathrm{3}\:{elements}\:{from} \\ $$$${H}\:{is}\:{divisible}\:{by}\:\mathrm{3},\:{there}\:{are}\:{following} \\ $$$${possibilities}: \\ $$$$\left.\mathrm{1}\right)\:{all}\:\mathrm{3}\:{elements}\:{are}\:{from}\:{H}_{\mathrm{3}} \:{or}\:{H}_{\mathrm{1}} \:{or}\:{H}_{\mathrm{2}} \\ $$$$\left.\mathrm{2}\right)\:{one}\:{element}\:{from}\:{H}_{\mathrm{1}} ,\:{one}\:{from}\:{H}_{\mathrm{2}} \\ $$$$\:\:\:\:\:{and}\:{one}\:{from}\:{H}_{\mathrm{3}} \\ $$$${total}\:{number}\:{of}\:{ways}: \\ $$$${x}=\mathrm{3}×{C}_{\mathrm{3}} ^{\mathrm{100}} +{C}_{\mathrm{1}} ^{\mathrm{100}} ×{C}_{\mathrm{1}} ^{\mathrm{100}} ×{C}_{\mathrm{1}} ^{\mathrm{100}} =\mathrm{1}\:\mathrm{485}\:\mathrm{100} \\ $$$${x}\:{mod}\:\mathrm{100000}\:=\mathrm{485}\:\mathrm{100} \\ $$
Commented by cortano12 last updated on 24/Feb/23
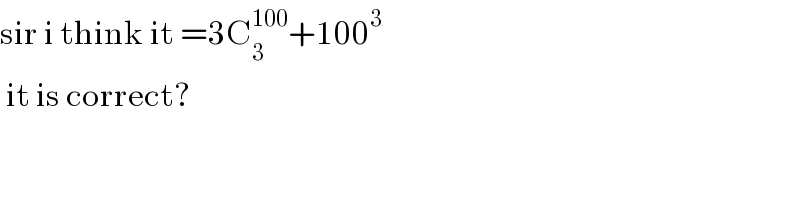
$$\mathrm{sir}\:\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:=\mathrm{3C}_{\mathrm{3}} ^{\mathrm{100}} +\mathrm{100}^{\mathrm{3}} \\ $$$$\:\mathrm{it}\:\mathrm{is}\:\mathrm{correct}? \\ $$
Commented by kapoorshah last updated on 24/Feb/23

$${wrong} \\ $$$$ \\ $$$${The}\:{possibilities}\:: \\ $$$$\left(\mathrm{1}\right)\:{all}\:\mathrm{3}\:{elements}\:{are}\:{from}\:{H}_{\mathrm{1}} \\ $$$$\left(\mathrm{2}\right)\:{all}\:\mathrm{3}\:{elements}\:{are}\:{from}\:{H}_{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:{all}\:\mathrm{3}\:{elements}\:{are}\:{from}\:{H}_{\mathrm{3}} \\ $$$$\left(\mathrm{4}\right)\:{one}\:{element}\:{from}\:{H}_{\mathrm{1}} ,\:{H}_{\mathrm{2}} ,\:{H}_{\mathrm{3}} \:{respectively} \\ $$$$\:{total}\:{number}\:{of}\:{ways}\:: \\ $$$${x}\:=\:\mathrm{3}×{C}_{\mathrm{3}} ^{\mathrm{100}} \:+\:{C}_{\mathrm{1}} ^{\mathrm{100}} \:×\:{C}_{\mathrm{1}} ^{\mathrm{100}} \:×\:{C}_{\mathrm{1}\:\:\:} ^{\mathrm{100}} \\ $$$$\:\:\:\:=\:\mathrm{1}\:\mathrm{485}\:\mathrm{100} \\ $$$$ \\ $$
Commented by mr W last updated on 24/Feb/23
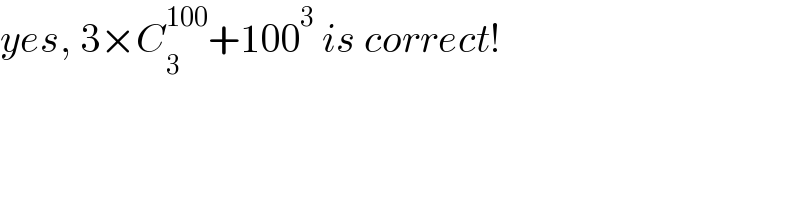
$${yes},\:\mathrm{3}×{C}_{\mathrm{3}} ^{\mathrm{100}} +\mathrm{100}^{\mathrm{3}} \:{is}\:{correct}! \\ $$
Commented by horsebrand11 last updated on 25/Feb/23

$${Yes}.. \\ $$
