
Question Number 187890 by Rupesh123 last updated on 23/Feb/23
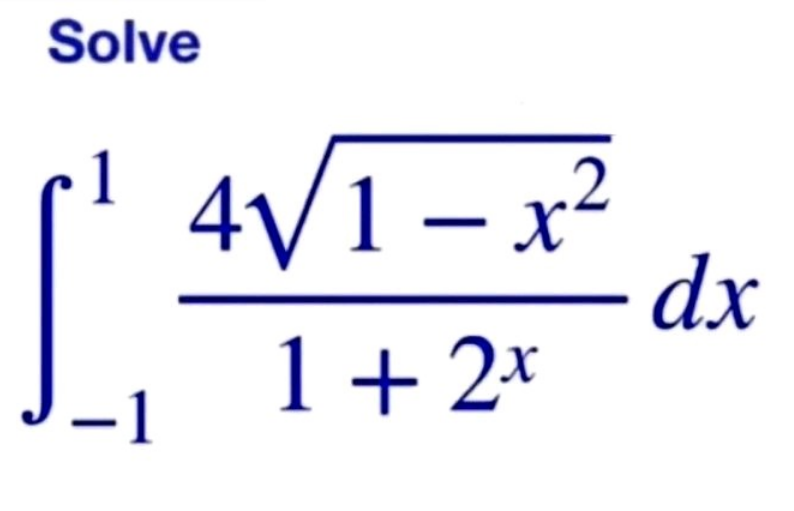
Answered by aleks041103 last updated on 23/Feb/23
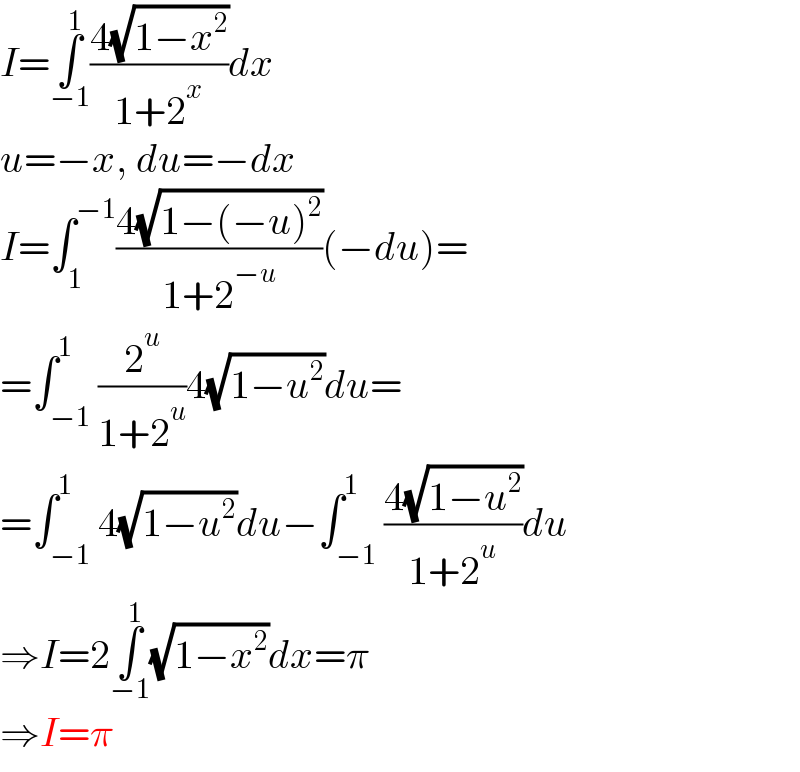
$${I}=\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{4}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{2}^{{x}} }{dx} \\ $$$${u}=−{x},\:{du}=−{dx} \\ $$$${I}=\int_{\mathrm{1}} ^{−\mathrm{1}} \frac{\mathrm{4}\sqrt{\mathrm{1}−\left(−{u}\right)^{\mathrm{2}} }}{\mathrm{1}+\mathrm{2}^{−{u}} }\left(−{du}\right)= \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{2}^{{u}} }{\mathrm{1}+\mathrm{2}^{{u}} }\mathrm{4}\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }{du}= \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{1}} \mathrm{4}\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }{du}−\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{4}\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{2}^{{u}} }{du} \\ $$$$\Rightarrow{I}=\mathrm{2}\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\pi \\ $$$$\Rightarrow{I}=\pi \\ $$
Commented by Rupesh123 last updated on 23/Feb/23
Perfect ��
