
Question Number 187819 by normans last updated on 22/Feb/23
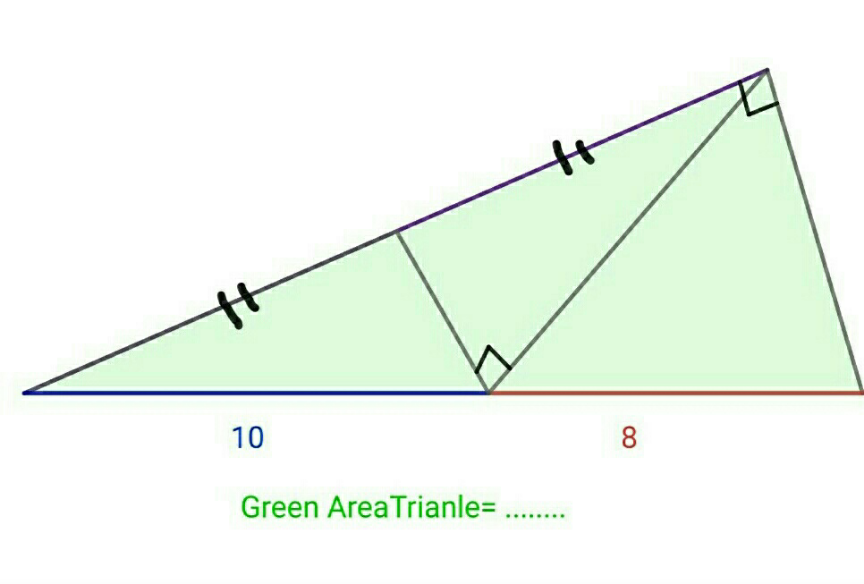
Answered by mr W last updated on 22/Feb/23
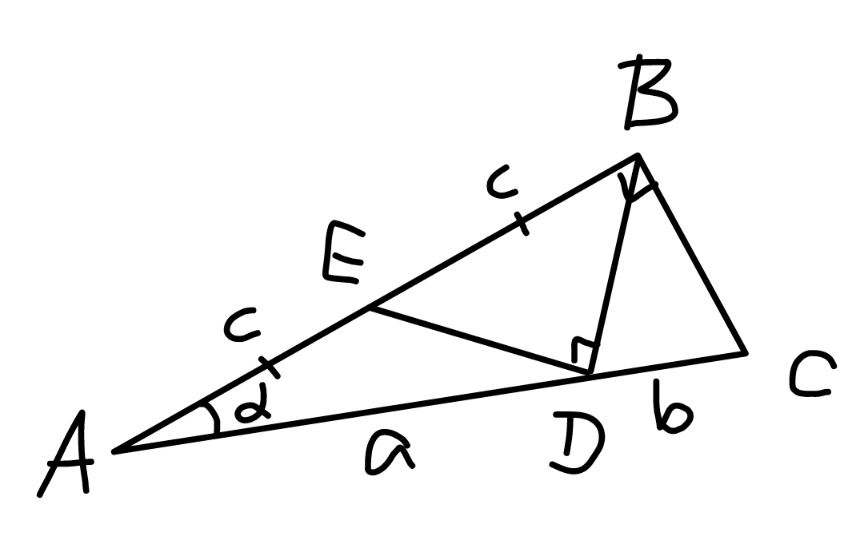
Commented by mr W last updated on 22/Feb/23

$${a}=\mathrm{10} \\ $$$${b}=\mathrm{8} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{2}{c}}{{a}+{b}} \\ $$$${ED}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}×\frac{\mathrm{2}{c}}{{a}+{b}} \\ $$$${BD}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} −\mathrm{4}{ac}×\frac{\mathrm{2}{c}}{{a}+{b}} \\ $$$${ED}^{\mathrm{2}} +{BD}^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}×\frac{\mathrm{2}{c}}{{a}+{b}}+{a}^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} −\mathrm{4}{ac}×\frac{\mathrm{2}{c}}{{a}+{b}}={c}^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} \left({a}+{b}\right)}{\mathrm{2}\left(\mathrm{2}{a}−{b}\right)} \\ $$$$\Rightarrow{c}={a}\sqrt{\frac{{a}+{b}}{\mathrm{2}\left(\mathrm{2}{a}−{b}\right)}} \\ $$$${BC}=\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\left(\mathrm{2}{c}\right)^{\mathrm{2}} }=\sqrt{\frac{{b}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\mathrm{2}{a}−{b}}} \\ $$$${area}\:{of}\:{triangle}\:{ABC}: \\ $$$$\Delta=\frac{\left(\mathrm{2}{c}\right)×{BC}}{\mathrm{2}}={a}\sqrt{\frac{{a}+{b}}{\mathrm{2}\left(\mathrm{2}{a}−{b}\right)}}\sqrt{\frac{{b}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}{\mathrm{2}{a}−{b}}} \\ $$$$\Delta=\frac{{a}\left({a}+{b}\right)}{\mathrm{2}{a}−{b}}\sqrt{\frac{{b}\left({a}−{b}\right)}{\mathrm{2}}} \\ $$$$\Delta=\frac{\mathrm{10}×\mathrm{18}}{\mathrm{12}}\sqrt{\frac{\mathrm{8}×\mathrm{2}}{\mathrm{2}}}=\mathrm{30}\sqrt{\mathrm{2}}\:\checkmark \\ $$
Commented by normans last updated on 22/Feb/23
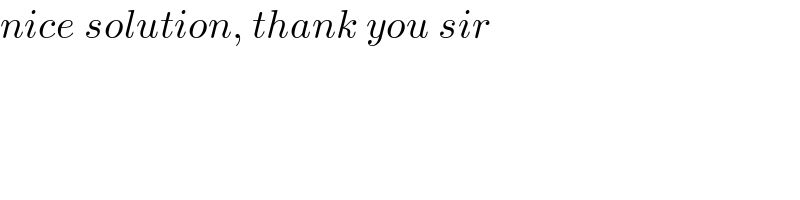
$${nice}\:{solution},\:{thank}\:{you}\:{sir} \\ $$
