
Question Number 187765 by Tawa11 last updated on 21/Feb/23
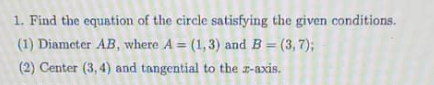
Answered by cortano12 last updated on 21/Feb/23
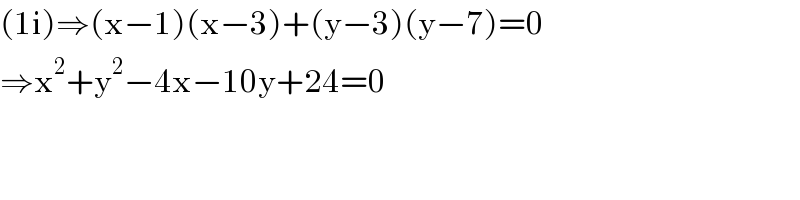
$$\left(\mathrm{1i}\right)\Rightarrow\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{3}\right)+\left(\mathrm{y}−\mathrm{3}\right)\left(\mathrm{y}−\mathrm{7}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{4x}−\mathrm{10y}+\mathrm{24}=\mathrm{0} \\ $$
Answered by cortano12 last updated on 21/Feb/23
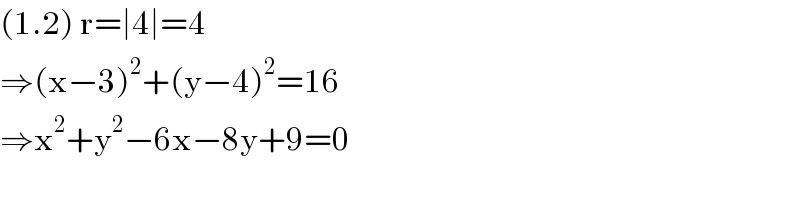
$$\left(\mathrm{1}.\mathrm{2}\right)\:\mathrm{r}=\mid\mathrm{4}\mid=\mathrm{4} \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{16} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{6x}−\mathrm{8y}+\mathrm{9}=\mathrm{0} \\ $$
Answered by floor(10²Eta[1]) last updated on 21/Feb/23
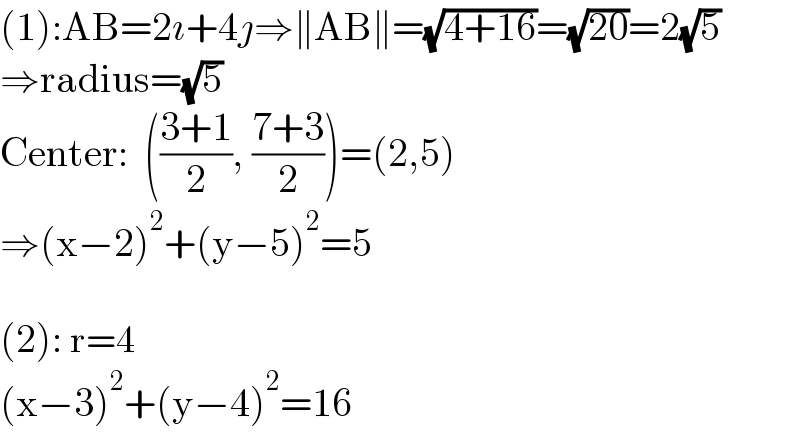
$$\left(\mathrm{1}\right):\mathrm{AB}=\mathrm{2}\imath+\mathrm{4}\jmath\Rightarrow\parallel\mathrm{AB}\parallel=\sqrt{\mathrm{4}+\mathrm{16}}=\sqrt{\mathrm{20}}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{radius}=\sqrt{\mathrm{5}} \\ $$$$\mathrm{Center}:\:\:\left(\frac{\mathrm{3}+\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{7}+\mathrm{3}}{\mathrm{2}}\right)=\left(\mathrm{2},\mathrm{5}\right) \\ $$$$\Rightarrow\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5} \\ $$$$ \\ $$$$\left(\mathrm{2}\right):\:\mathrm{r}=\mathrm{4} \\ $$$$\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{16} \\ $$
