
Question Number 187760 by pascal889 last updated on 21/Feb/23

Commented by Frix last updated on 21/Feb/23
$$\mathrm{You}\:\mathrm{posted}\:\mathrm{this}\:\mathrm{before}\:\mathrm{in}\:\mathrm{question}\:\mathrm{186750} \\ $$
Commented by pascal889 last updated on 21/Feb/23
$${please}\:{can}\:{u}\:{explsin}\:{it}\:{better}\:{sir} \\ $$
Answered by Sutrisno last updated on 24/Feb/23
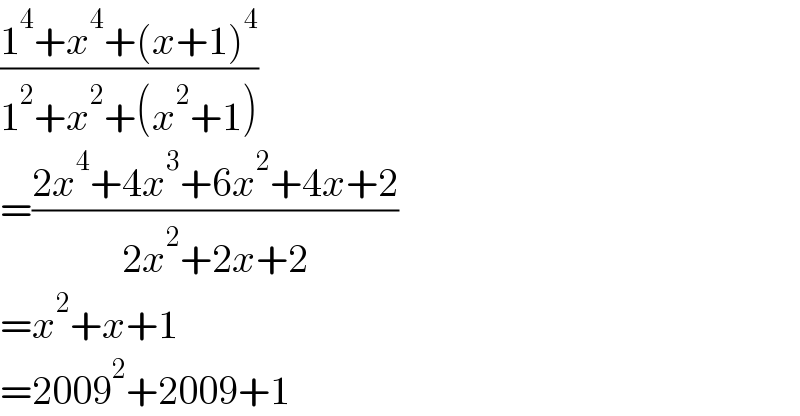
$$\frac{\mathrm{1}^{\mathrm{4}} +{x}^{\mathrm{4}} +\left({x}+\mathrm{1}\right)^{\mathrm{4}} }{\mathrm{1}^{\mathrm{2}} +{x}^{\mathrm{2}} +\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} +{x}+\mathrm{1} \\ $$$$=\mathrm{2009}^{\mathrm{2}} +\mathrm{2009}+\mathrm{1} \\ $$
