Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 187703 by Tawa11 last updated on 20/Feb/23

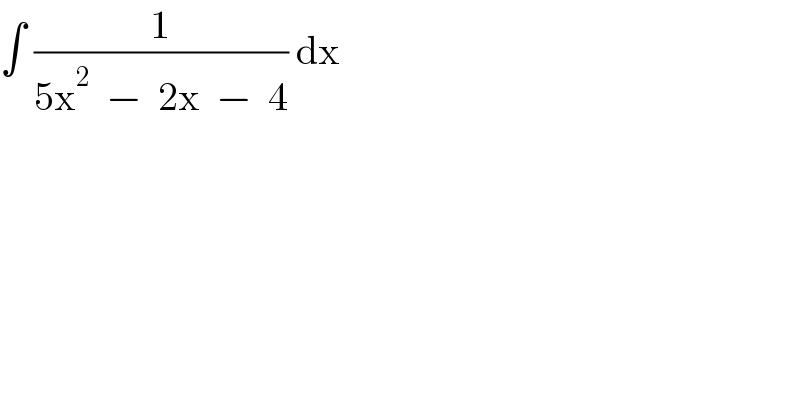
∫ (1/(5x^2 − 2x − 4)) dx

$$\int\:\frac{\mathrm{1}}{\mathrm{5x}^{\mathrm{2}} \:\:−\:\:\mathrm{2x}\:\:−\:\:\mathrm{4}}\:\mathrm{dx} \\ $$

Answered by MikeH last updated on 20/Feb/23

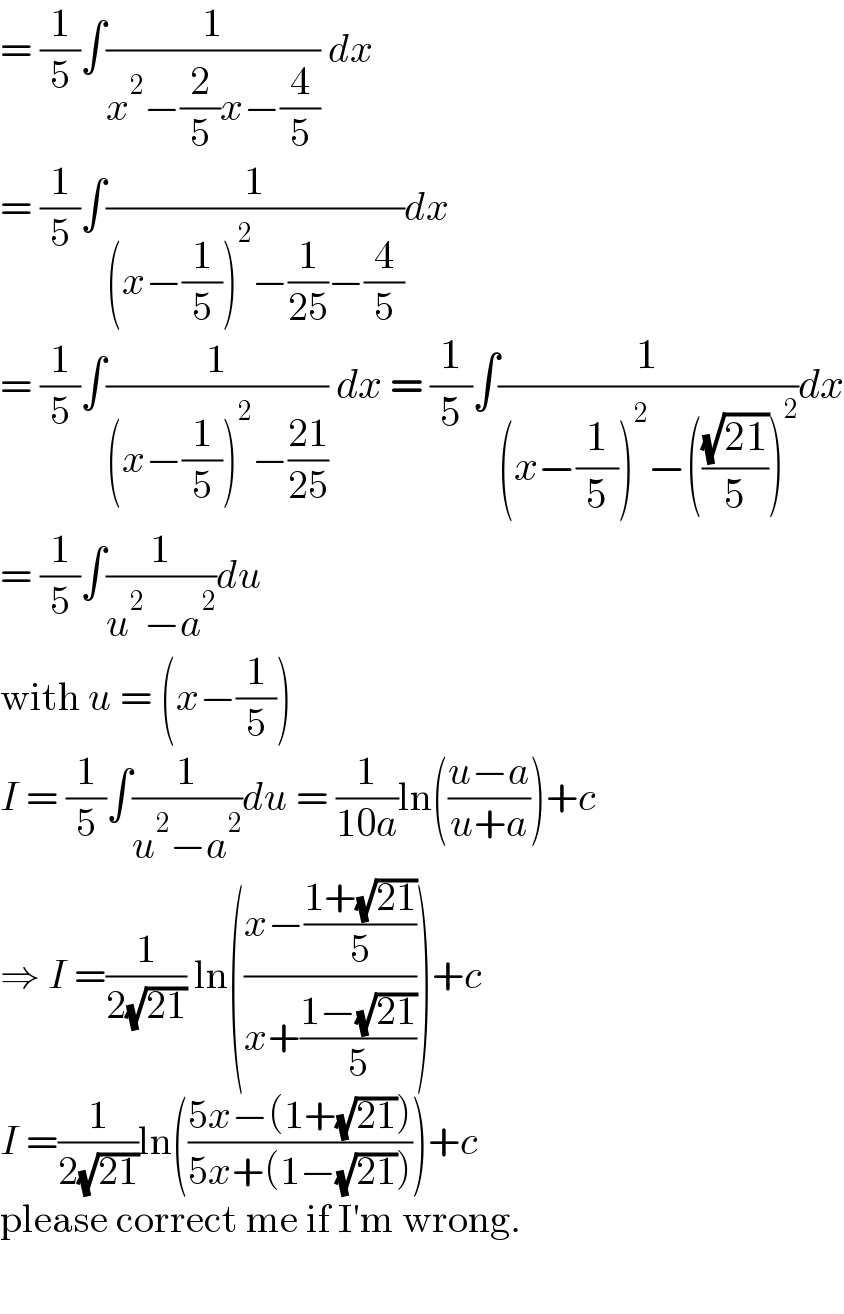
= (1/5)∫(1/(x^2 −(2/5)x−(4/5))) dx = (1/5)∫(1/((x−(1/5))^2 −(1/(25))−(4/5)))dx = (1/5)∫(1/((x−(1/5))^2 −((21)/(25)))) dx = (1/5)∫(1/((x−(1/5))^2 −(((√(21))/5))^2 ))dx = (1/5)∫(1/(u^2 −a^2 ))du with u = (x−(1/5)) I = (1/5)∫(1/(u^2 −a^2 ))du = (1/(10a))ln(((u−a)/(u+a)))+c ⇒ I =(1/(2(√(21)))) ln(((x−((1+(√(21)))/5))/(x+((1−(√(21)))/5))))+c I =(1/(2(√(21))))ln(((5x−(1+(√(21))))/(5x+(1−(√(21))))))+c please correct me if I′m wrong.

$$=\:\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{5}}{x}−\frac{\mathrm{4}}{\mathrm{5}}}\:{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{25}}−\frac{\mathrm{4}}{\mathrm{5}}}{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} −\frac{\mathrm{21}}{\mathrm{25}}}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{21}}}{\mathrm{5}}\right)^{\mathrm{2}} }{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} −{a}^{\mathrm{2}} }{du}\: \\ $$$$\mathrm{with}\:{u}\:=\:\left({x}−\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} −{a}^{\mathrm{2}} }{du}\:=\:\frac{\mathrm{1}}{\mathrm{10}{a}}\mathrm{ln}\left(\frac{{u}−{a}}{{u}+{a}}\right)+{c} \\ $$$$\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{21}}}\:\mathrm{ln}\left(\frac{{x}−\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{5}}}{{x}+\frac{\mathrm{1}−\sqrt{\mathrm{21}}}{\mathrm{5}}}\right)+{c} \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{21}}}\mathrm{ln}\left(\frac{\mathrm{5}{x}−\left(\mathrm{1}+\sqrt{\mathrm{21}}\right)}{\mathrm{5}{x}+\left(\mathrm{1}−\sqrt{\mathrm{21}}\right)}\right)+{c} \\ $$$$\mathrm{please}\:\mathrm{correct}\:\mathrm{me}\:\mathrm{if}\:\mathrm{I}'\mathrm{m}\:\mathrm{wrong}.\: \\ $$$$ \\ $$

Commented by Ar Brandon last updated on 20/Feb/23

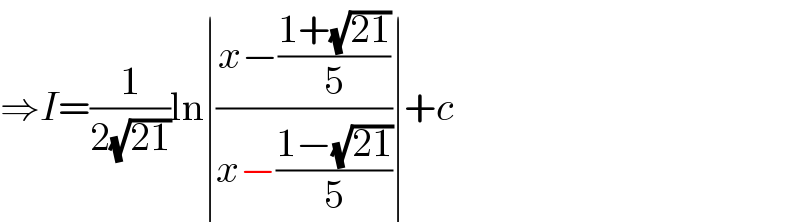
⇒I=(1/(2(√(21))))ln∣((x−((1+(√(21)))/5))/(x−((1−(√(21)))/5)))∣+c

$$\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{21}}}\mathrm{ln}\mid\frac{{x}−\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{5}}}{{x}−\frac{\mathrm{1}−\sqrt{\mathrm{21}}}{\mathrm{5}}}\mid+{c} \\ $$

Answered by Nimnim111118 last updated on 21/Feb/23

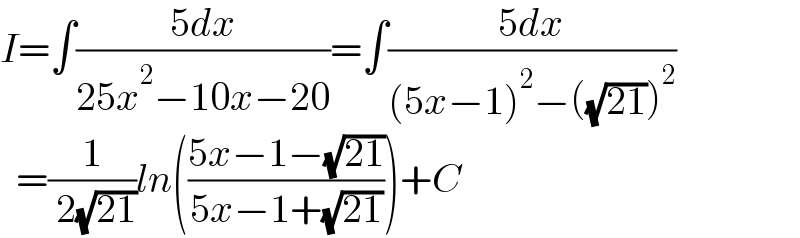
I=∫((5dx)/(25x^2 −10x−20))=∫((5dx)/((5x−1)^2 −((√(21)))^2 )) =(1/( 2(√(21))))ln(((5x−1−(√(21)))/(5x−1+(√(21)))))+C

$${I}=\int\frac{\mathrm{5}{dx}}{\mathrm{25}{x}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{20}}=\int\frac{\mathrm{5}{dx}}{\left(\mathrm{5}{x}−\mathrm{1}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{21}}\right)^{\mathrm{2}} } \\ $$$$\:\:=\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{21}}}{ln}\left(\frac{\mathrm{5}{x}−\mathrm{1}−\sqrt{\mathrm{21}}}{\mathrm{5}{x}−\mathrm{1}+\sqrt{\mathrm{21}}}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com