
Question Number 187683 by 073 last updated on 20/Feb/23
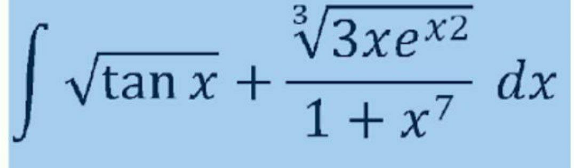
Answered by anurup last updated on 20/Feb/23
![I_1 =∫(√(tan x)) dx =(1/2)∫{((√(tan x)) +(√(cot x)) )+((√(tan x)) −(√(cot x)))}dx =(1/2)∫{((√((sin x)/(cos x))) +(√((cos x)/(sin x))))+ ((√((sin x)/(cos x))) −(√((cos x)/(sin x))) )}dx =(1/2)∫{(((sin x+cos x)/( (√(sin xcos x)))))+(((sin x−cos x)/( (√(sin xcos x)))))}dx =(1/( (√2)))∫{(((sin x+cos x)/( (√(2sin xcos x)))))+(((sin x−cos x)/( (√(2sin xcos x)))))}dx =(1/( (√2)))∫{(((sin x+cos x)/( (√(1−(1−2sin xcos x))))))+(((sin x−cos x)/( (√((1+2sin xcos x)−1)))))}dx =(1/( (√2)))∫{(((sin x+cos x)/( (√(1−(sin x−cos x)^2 )))))−(((cos x−sin x)/( (√((sin x+cos x)^2 −1)))))}dx =(1/( (√(2 )) ))∫(du/( (√(1−u^(2 ) ))))−(1/( (√2)))∫(dv/( (√(v^2 −1)))) [u=sin x−cos x, v=sin x+cos x] =(1/( (√2)))sin^(−1) (u)−(1/( (√2)))ln ∣v+(√(v^2 −1)) ∣+C_1 =(1/( (√2)))sin^(−1) (sin x−cos x)−(1/( (√2)))ln ∣sin x+cos x+(√(sin 2x)) ∣+C_1 I_(2 ) =∫(((3xe^x^2 ))^(1/3) /(1+x^7 ))dx =∫(((3x)^(1/3) e^(x^2 /3) )/(1+x^7 ))dx](Q187719.png)
$$\mathrm{I}_{\mathrm{1}} =\int\sqrt{\mathrm{tan}\:{x}}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\left(\sqrt{\mathrm{tan}\:{x}}\:+\sqrt{\mathrm{cot}\:{x}}\:\right)+\left(\sqrt{\mathrm{tan}\:{x}}\:−\sqrt{\mathrm{cot}\:{x}}\right)\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\left(\sqrt{\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}}\:+\sqrt{\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}}\right)+\:\left(\sqrt{\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}}\:−\sqrt{\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}}\:\right)\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\left(\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{sin}\:{x}\mathrm{cos}\:{x}}}\right)+\left(\frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{sin}\:{x}\mathrm{cos}\:{x}}}\right)\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\left\{\left(\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{2sin}\:{x}\mathrm{cos}\:{x}}}\right)+\left(\frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{2sin}\:{x}\mathrm{cos}\:{x}}}\right)\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\left\{\left(\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:{x}\mathrm{cos}\:{x}\right)}}\right)+\left(\frac{\mathrm{sin}\:{x}−\mathrm{cos}\:{x}}{\:\sqrt{\left(\mathrm{1}+\mathrm{2sin}\:{x}\mathrm{cos}\:{x}\right)−\mathrm{1}}}\right)\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\left\{\left(\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{1}−\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)^{\mathrm{2}} }}\right)−\left(\frac{\mathrm{cos}\:{x}−\mathrm{sin}\:\:{x}}{\:\sqrt{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} −\mathrm{1}}}\right)\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\:}\:}\int\frac{{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}\:} }}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dv}}{\:\sqrt{{v}^{\mathrm{2}} −\mathrm{1}}}\:\left[{u}=\mathrm{sin}\:{x}−\mathrm{cos}\:{x},\:{v}=\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{sin}^{−\mathrm{1}} \left({u}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid{v}+\sqrt{{v}^{\mathrm{2}} −\mathrm{1}}\:\mid+\mathrm{C}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\sqrt{\mathrm{sin}\:\mathrm{2}{x}}\:\mid+\mathrm{C}_{\mathrm{1}} \\ $$$$\mathrm{I}_{\mathrm{2}\:} =\int\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}{xe}^{{x}^{\mathrm{2}} } }}{\mathrm{1}+{x}^{\mathrm{7}} }{dx} \\ $$$$=\int\frac{\left(\mathrm{3}{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{3}}} }{\mathrm{1}+{x}^{\mathrm{7}} }{dx} \\ $$$$ \\ $$
Commented by anurup last updated on 20/Feb/23

$$\mathrm{I}_{\mathrm{2}} \:\mathrm{not}\:\mathrm{done} \\ $$
Commented by 073 last updated on 21/Feb/23

$$\mathrm{thanks}\:\mathrm{alot} \\ $$
