
Question Number 187524 by sonukgindia last updated on 18/Feb/23
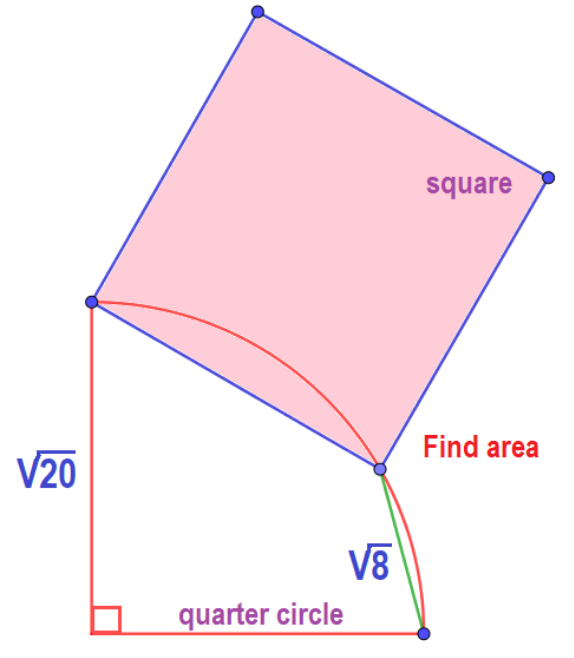
Answered by HeferH last updated on 18/Feb/23
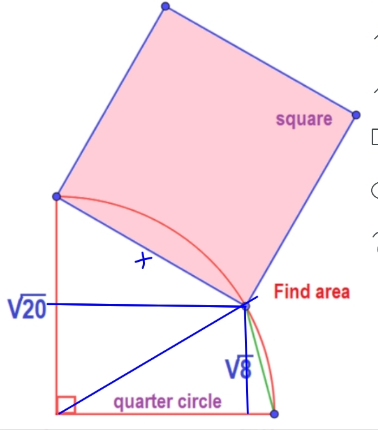
Commented by HeferH last updated on 18/Feb/23

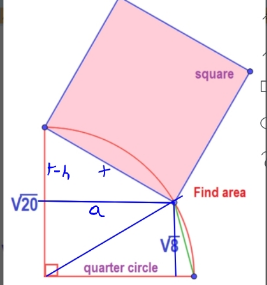
$$\:{Area}\:{of}\:{triangle}\:\left(\sqrt{\mathrm{20}},\sqrt{\mathrm{20}},\sqrt{\mathrm{8}}\right)=\:{A} \\ $$$$\:{A}\:=\:\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}\:\left({Heron}\right) \\ $$$$\:{A}=\:\sqrt{\left(\mathrm{2}\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{2}}\right)\left(\mathrm{2}\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}\right)} \\ $$$$\:{A}\:=\:\sqrt{\left(\mathrm{20}−\mathrm{2}\right)\mathrm{2}}\:=\:\mathrm{6}\: \\ $$$$\:{but}\:{also}:\:\:{A}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{5}}\centerdot{h}}{\mathrm{2}}\:=\:\mathrm{6} \\ $$$$\:{h}\:=\:\frac{\mathrm{6}}{\:\sqrt{\mathrm{5}}}\:=\:\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}} \\ $$$$\:{a}^{\mathrm{2}} =\:{r}^{\mathrm{2}} −{h}^{\mathrm{2}} \\ $$$$\:{a}^{\mathrm{2}} +\left({r}−{h}\right)^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} \\ $$$$\:\mathrm{2}{r}^{\mathrm{2}} −\mathrm{2}{rh}={x}^{\mathrm{2}} \\ $$$$\:\mathrm{2}\left(\mathrm{20}\right)−\mathrm{2}\sqrt{\mathrm{20}}\centerdot\frac{\mathrm{6}\sqrt{\mathrm{5}}}{\mathrm{5}}\:=\:{x}^{\mathrm{2}} \\ $$$$\:\mathrm{40}−\mathrm{24}={x}^{\mathrm{2}} \\ $$$$\:\mathrm{16}\:=\:{x}^{\mathrm{2}} \\ $$
Commented by HeferH last updated on 18/Feb/23
Answered by mr W last updated on 18/Feb/23
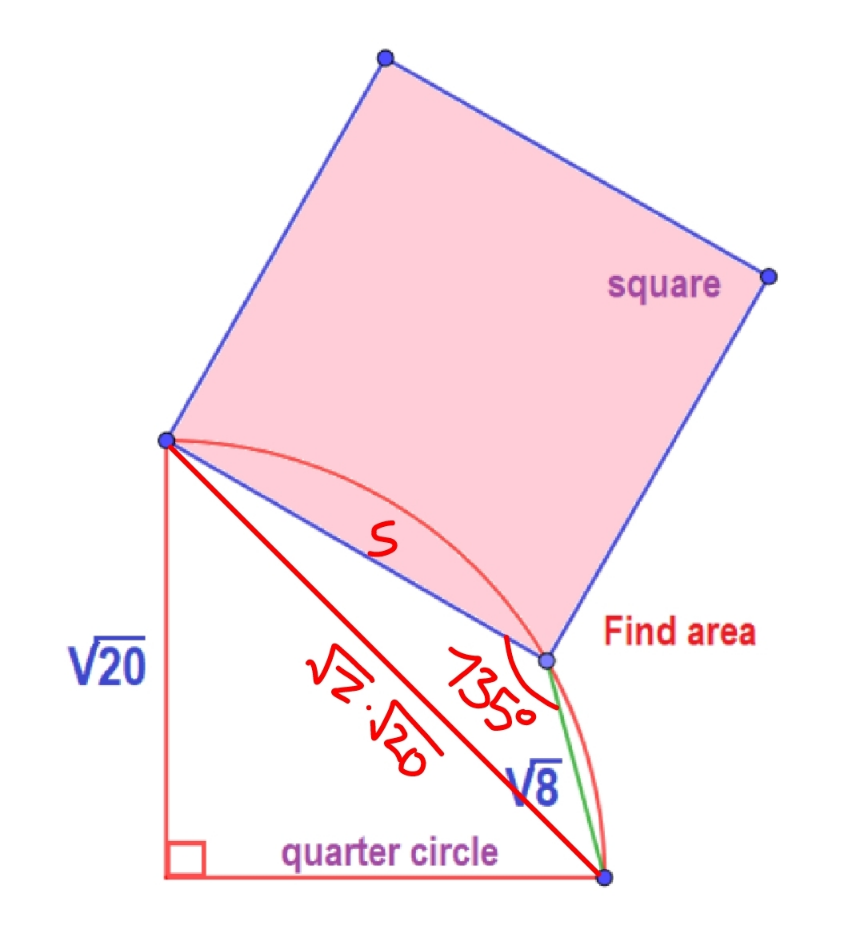
Commented by mr W last updated on 18/Feb/23
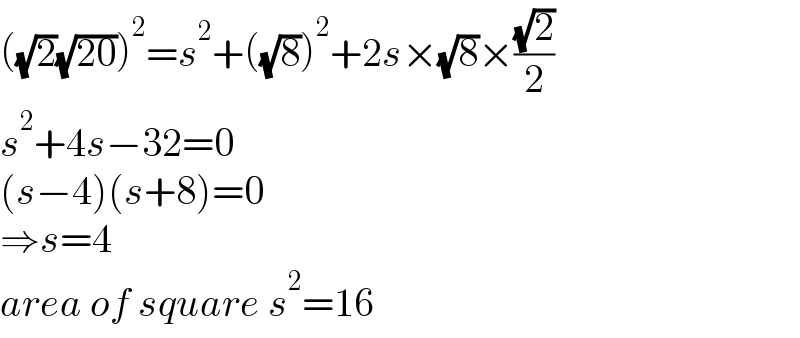
$$\left(\sqrt{\mathrm{2}}\sqrt{\mathrm{20}}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} +\left(\sqrt{\mathrm{8}}\right)^{\mathrm{2}} +\mathrm{2}{s}×\sqrt{\mathrm{8}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} +\mathrm{4}{s}−\mathrm{32}=\mathrm{0} \\ $$$$\left({s}−\mathrm{4}\right)\left({s}+\mathrm{8}\right)=\mathrm{0} \\ $$$$\Rightarrow{s}=\mathrm{4} \\ $$$${area}\:{of}\:{square}\:{s}^{\mathrm{2}} =\mathrm{16} \\ $$
