
Question Number 187433 by Mastermind last updated on 17/Feb/23

$$\mathrm{Prove}\:\mathrm{that}\:\bigtriangledown×\bigtriangledown\phi=\mathrm{0}.\:\mathrm{If}\:\phi\:\mathrm{is} \\ $$$$\mathrm{assumed}\:\mathrm{to}\:\mathrm{be}\:\mathrm{continous}\:\mathrm{and} \\ $$$$\mathrm{having}\:\mathrm{continous}\:\mathrm{first}\:\mathrm{and}\:\mathrm{second} \\ $$$$\mathrm{order}\:\mathrm{derivatives}. \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Answered by aleks041103 last updated on 17/Feb/23
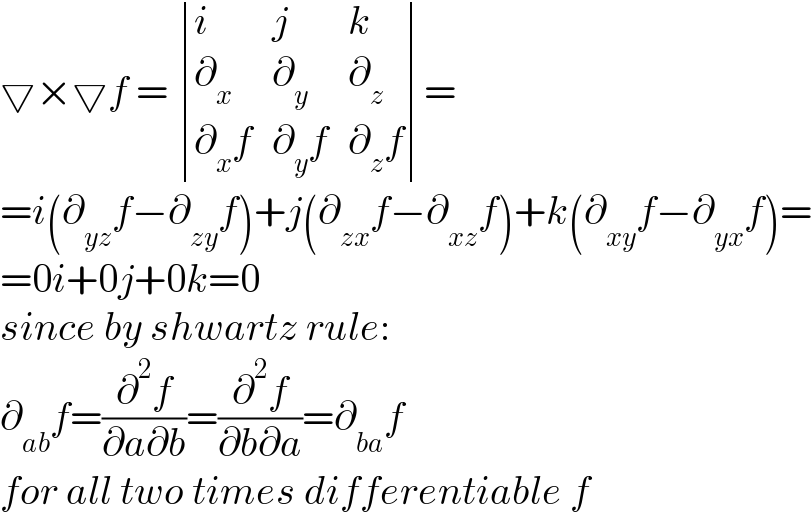
$$\bigtriangledown×\bigtriangledown{f}\:=\:\begin{vmatrix}{{i}}&{{j}}&{{k}}\\{\partial_{{x}} }&{\partial_{{y}} }&{\partial_{{z}} }\\{\partial_{{x}} {f}}&{\partial_{{y}} {f}}&{\partial_{{z}} {f}}\end{vmatrix}= \\ $$$$={i}\left(\partial_{{yz}} {f}−\partial_{{zy}} {f}\right)+{j}\left(\partial_{{zx}} {f}−\partial_{{xz}} {f}\right)+{k}\left(\partial_{{xy}} {f}−\partial_{{yx}} {f}\right)= \\ $$$$=\mathrm{0}{i}+\mathrm{0}{j}+\mathrm{0}{k}=\mathrm{0} \\ $$$${since}\:{by}\:{shwartz}\:{rule}: \\ $$$$\partial_{{ab}} {f}=\frac{\partial^{\mathrm{2}} {f}}{\partial{a}\partial{b}}=\frac{\partial^{\mathrm{2}} {f}}{\partial{b}\partial{a}}=\partial_{{ba}} {f} \\ $$$${for}\:{all}\:{two}\:{times}\:{differentiable}\:{f} \\ $$
Commented by Mastermind last updated on 17/Feb/23
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{BOSS} \\ $$
