
Question Number 187406 by Fridunatjan08 last updated on 16/Feb/23
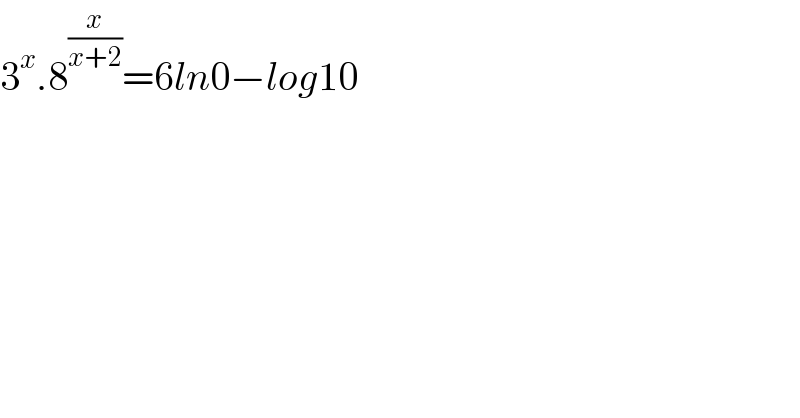
$$\mathrm{3}^{{x}} .\mathrm{8}^{\frac{{x}}{{x}+\mathrm{2}}} =\mathrm{6}{ln}\mathrm{0}−{log}\mathrm{10} \\ $$
Commented by Fridunatjan08 last updated on 16/Feb/23
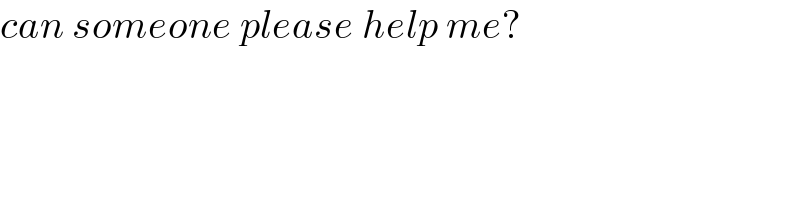
$${can}\:{someone}\:{please}\:{help}\:{me}? \\ $$
Commented by Frix last updated on 17/Feb/23

$$\mathrm{ln}\:\mathrm{0}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined} \\ $$
Answered by a.lgnaoui last updated on 17/Feb/23
![Ithink that you want to tel 6ln10 we suppose that thrue log10=((ln10)/(ln10))=1 3^x .8^(x/(x+2)) =6ln10−1 a=b (a>0 b>0⇒lna=lnb xln3+(x/(x+2))ln8=ln[6ln10−1] posons k=ln[6ln10−1] x(x+2)ln3+xln8=(x+2)k x^2 ln3+2xln3+xln8=(x+2)k x^2 ln3+x(2ln3+ln8−k)−2k=0 x^2 +(1/(ln3))(2ln3+3ln2−k)x−((2k)/(ln3))=0 [x+(1+((3ln2−k)/(2ln3)))]^2 − [1+((3ln2−k)/(2ln3)))^2 +((2k)/(ln3))]=0 x+(1+((3ln2−k)/(2ln3)))= (√((1+((3ln2−k)/(2ln3)))^2 +((2k)/(ln3)))) x=±(√((1+((3ln2−k)/(2ln3)))^2 +((2k)/(ln3)))) −1−((3kn2−k)/(2ln3))](Q187413.png)
$${Ithink}\:{that}\:{you}\:{want}\:{to}\:{tel}\:\mathrm{6}{ln}\mathrm{10} \\ $$$${we}\:{suppose}\:{that}\:{thrue} \\ $$$${log}\mathrm{10}=\frac{{ln}\mathrm{10}}{{ln}\mathrm{10}}=\mathrm{1} \\ $$$$\mathrm{3}^{{x}} .\mathrm{8}^{\frac{{x}}{{x}+\mathrm{2}}} =\mathrm{6}{ln}\mathrm{10}−\mathrm{1} \\ $$$${a}={b}\:\:\left({a}>\mathrm{0}\:{b}>\mathrm{0}\Rightarrow{lna}={lnb}\right. \\ $$$${xln}\mathrm{3}+\frac{{x}}{{x}+\mathrm{2}}{ln}\mathrm{8}={ln}\left[\mathrm{6}{ln}\mathrm{10}−\mathrm{1}\right] \\ $$$${posons}\:\:\:{k}={ln}\left[\mathrm{6}{ln}\mathrm{10}−\mathrm{1}\right] \\ $$$${x}\left({x}+\mathrm{2}\right){ln}\mathrm{3}+{xln}\mathrm{8}=\left({x}+\mathrm{2}\right){k} \\ $$$${x}^{\mathrm{2}} {ln}\mathrm{3}+\mathrm{2}{xln}\mathrm{3}+{xln}\mathrm{8}=\left({x}+\mathrm{2}\right){k} \\ $$$${x}^{\mathrm{2}} {ln}\mathrm{3}+{x}\left(\mathrm{2}{ln}\mathrm{3}+{ln}\mathrm{8}−{k}\right)−\mathrm{2}{k}=\mathrm{0} \\ $$$$ \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} +\frac{\mathrm{1}}{{ln}\mathrm{3}}\left(\mathrm{2}{ln}\mathrm{3}+\mathrm{3}{ln}\mathrm{2}−{k}\right)\boldsymbol{{x}}−\frac{\mathrm{2}{k}}{{ln}\mathrm{3}}=\mathrm{0} \\ $$$$\left[\boldsymbol{{x}}+\left(\mathrm{1}+\frac{\mathrm{3}{ln}\mathrm{2}−{k}}{\mathrm{2}{ln}\mathrm{3}}\right)\right]^{\mathrm{2}} − \\ $$$$\left.\left[\mathrm{1}+\frac{\mathrm{3}{ln}\mathrm{2}−{k}}{\mathrm{2}{ln}\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{2}{k}}{{ln}\mathrm{3}}\right]=\mathrm{0} \\ $$$$ \\ $$$${x}+\left(\mathrm{1}+\frac{\mathrm{3}{ln}\mathrm{2}−{k}}{\mathrm{2}{ln}\mathrm{3}}\right)= \\ $$$$\sqrt{\left(\mathrm{1}+\frac{\mathrm{3}{ln}\mathrm{2}−{k}}{\mathrm{2}{ln}\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{2}{k}}{{ln}\mathrm{3}}} \\ $$$$ \\ $$$$\boldsymbol{{x}}=\pm\sqrt{\left(\mathrm{1}+\frac{\mathrm{3}{ln}\mathrm{2}−{k}}{\mathrm{2}{ln}\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{2}{k}}{{ln}\mathrm{3}}}\:−\mathrm{1}−\frac{\mathrm{3}{kn}\mathrm{2}−{k}}{\mathrm{2}{ln}\mathrm{3}} \\ $$
Commented by Fridunatjan08 last updated on 17/Feb/23

$${thsnks}\:{you}\:{bro}. \\ $$
