Question and Answers Forum

All Question   Topic List

Question Number 187390 by mathlove last updated on 18/Feb/23

odd number (2n+1)

$${odd}\:{number}\:\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$ The sum of twelve consecutive natural numbers is 288. Find the largest natural number\\n

Answered by JDamian last updated on 16/Feb/23

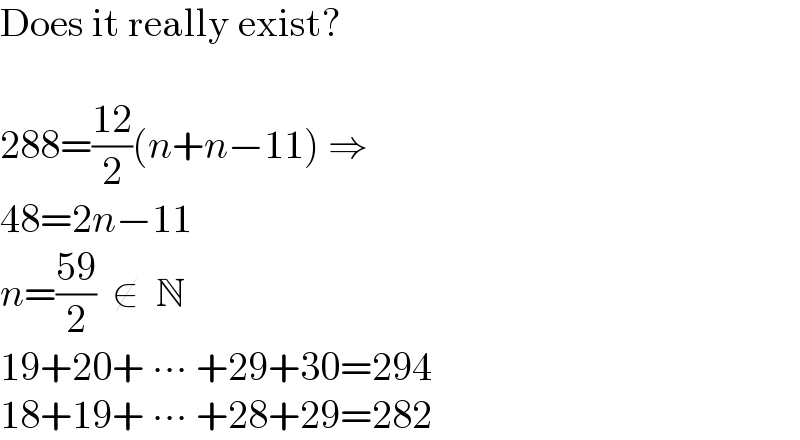
Does it really exist? 288=((12)/2)(n+n−11) ⇒ 48=2n−11 n=((59)/2) ∉ N 19+20+ ∙∙∙ +29+30=294 18+19+ ∙∙∙ +28+29=282

$$\mathrm{Does}\:\mathrm{it}\:\mathrm{really}\:\mathrm{exist}? \\ $$ $$ \\ $$ $$\mathrm{288}=\frac{\mathrm{12}}{\mathrm{2}}\left({n}+{n}−\mathrm{11}\right)\:\Rightarrow\: \\ $$ $$\mathrm{48}=\mathrm{2}{n}−\mathrm{11} \\ $$ $${n}=\frac{\mathrm{59}}{\mathrm{2}}\:\:\notin\:\:\mathbb{N} \\ $$ $$\mathrm{19}+\mathrm{20}+\:\centerdot\centerdot\centerdot\:+\mathrm{29}+\mathrm{30}=\mathrm{294} \\ $$ $$\mathrm{18}+\mathrm{19}+\:\centerdot\centerdot\centerdot\:+\mathrm{28}+\mathrm{29}=\mathrm{282} \\ $$

Commented bymathlove last updated on 16/Feb/23

n=12 find a_n

$${n}=\mathrm{12}\:\:{find}\:{a}_{{n}} \\ $$

Commented byJDamian last updated on 16/Feb/23

there is no such natural number a_n

Commented byMathsFan last updated on 17/Feb/23

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented bymathlove last updated on 17/Feb/23

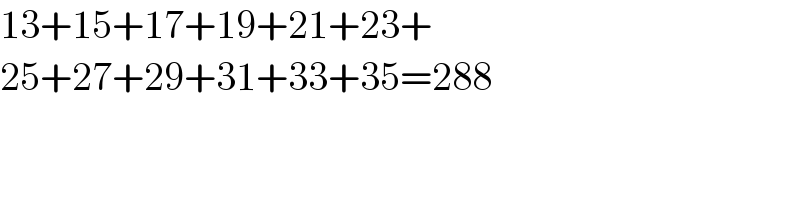
13+15+17+19+21+23+ 25+27+29+31+33+35=288

$$\mathrm{13}+\mathrm{15}+\mathrm{17}+\mathrm{19}+\mathrm{21}+\mathrm{23}+ \\ $$ $$\mathrm{25}+\mathrm{27}+\mathrm{29}+\mathrm{31}+\mathrm{33}+\mathrm{35}=\mathrm{288} \\ $$

Commented bymr W last updated on 17/Feb/23

then your question is wrong!

$${then}\:{your}\:{question}\:{is}\:{wrong}! \\ $$

Commented byJDamian last updated on 19/Feb/23

Mathlove, do you even check your questions and solutions before posting them?

Answered by HeferH last updated on 16/Feb/23

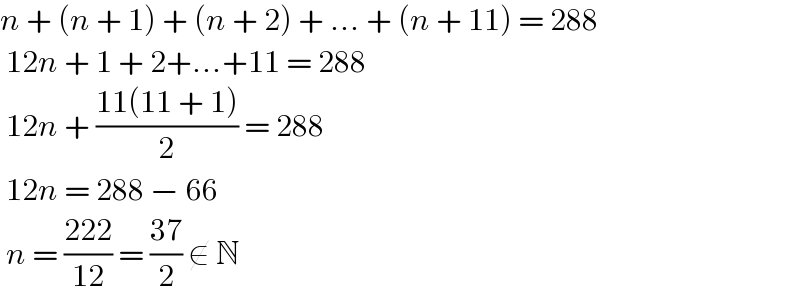
n + (n + 1) + (n + 2) + ... + (n + 11) = 288 12n + 1 + 2+...+11 = 288 12n + ((11(11 + 1))/2) = 288 12n = 288 − 66 n = ((222)/(12)) = ((37)/2) ∉ N

$${n}\:+\:\left({n}\:+\:\mathrm{1}\right)\:+\:\left({n}\:+\:\mathrm{2}\right)\:+\:...\:+\:\left({n}\:+\:\mathrm{11}\right)\:=\:\mathrm{288} \\ $$ $$\:\mathrm{12}{n}\:+\:\mathrm{1}\:+\:\mathrm{2}+...+\mathrm{11}\:=\:\mathrm{288} \\ $$ $$\:\mathrm{12}{n}\:+\:\frac{\mathrm{11}\left(\mathrm{11}\:+\:\mathrm{1}\right)}{\mathrm{2}}\:=\:\mathrm{288} \\ $$ $$\:\mathrm{12}{n}\:=\:\mathrm{288}\:−\:\mathrm{66} \\ $$ $$\:{n}\:=\:\frac{\mathrm{222}}{\mathrm{12}}\:=\:\frac{\mathrm{37}}{\mathrm{2}}\:\notin\:\mathbb{N}\: \\ $$

Commented byMathsFan last updated on 17/Feb/23

thanks a lot sir

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com