
Question Number 187381 by a.lgnaoui last updated on 16/Feb/23
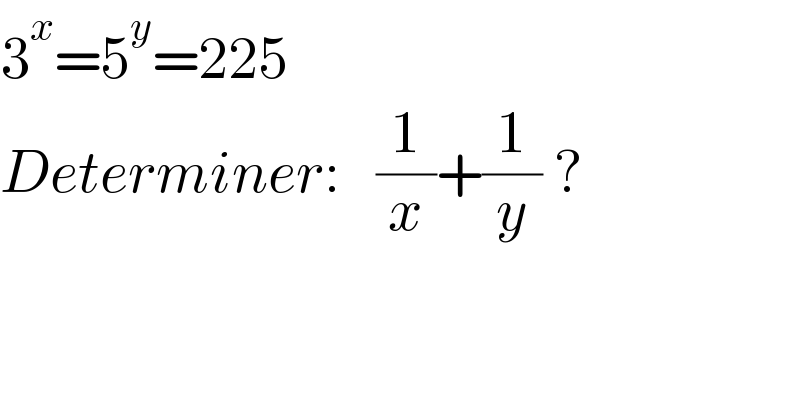
$$\mathrm{3}^{{x}} =\mathrm{5}^{{y}} =\mathrm{225} \\ $$$${Determiner}:\:\:\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\:? \\ $$
Answered by horsebrand11 last updated on 16/Feb/23
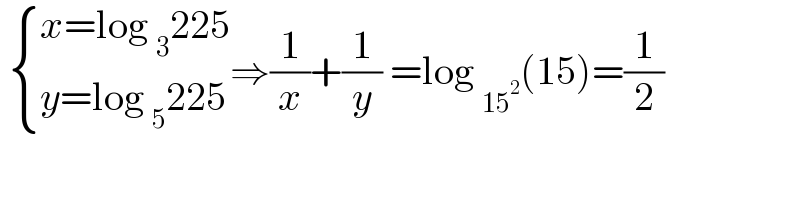
$$\:\begin{cases}{{x}=\mathrm{log}\:_{\mathrm{3}} \mathrm{225}}\\{{y}=\mathrm{log}\:_{\mathrm{5}} \mathrm{225}}\end{cases}\Rightarrow\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\:=\mathrm{log}\:_{\mathrm{15}^{\mathrm{2}} } \left(\mathrm{15}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by a.lgnaoui last updated on 16/Feb/23

$${thanks} \\ $$
Answered by anurup last updated on 17/Feb/23
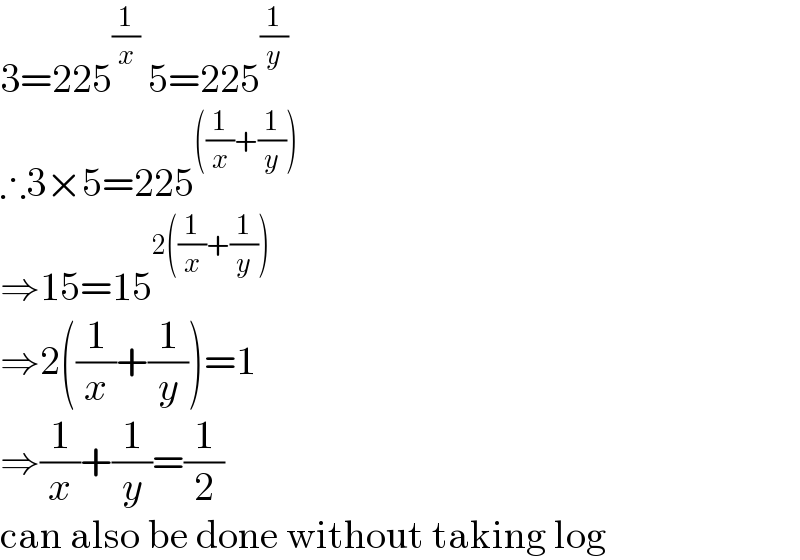
$$\mathrm{3}=\mathrm{225}^{\frac{\mathrm{1}}{{x}}} \:\mathrm{5}=\mathrm{225}^{\frac{\mathrm{1}}{{y}}} \\ $$$$\therefore\mathrm{3}×\mathrm{5}=\mathrm{225}^{\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right)} \\ $$$$\Rightarrow\mathrm{15}=\mathrm{15}^{\mathrm{2}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right)} \\ $$$$\Rightarrow\mathrm{2}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right)=\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{can}\:\mathrm{also}\:\mathrm{be}\:\mathrm{done}\:\mathrm{without}\:\mathrm{taking}\:\mathrm{log} \\ $$
