
Question Number 187359 by Humble last updated on 16/Feb/23
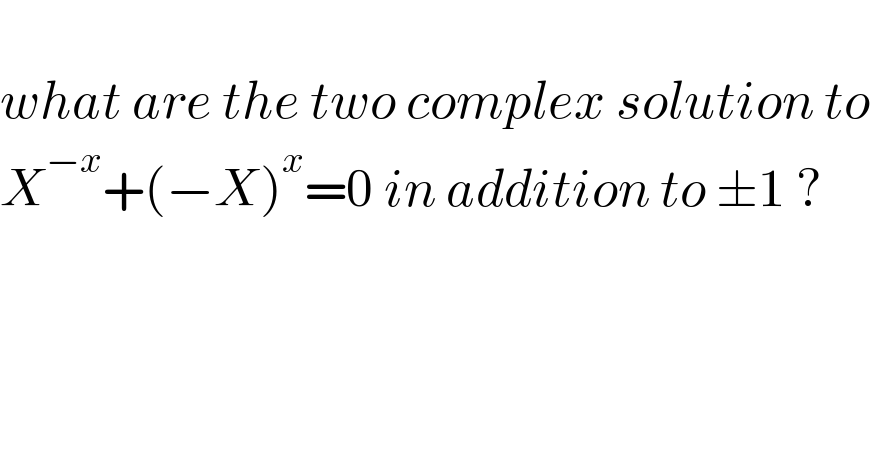
$$ \\ $$$${what}\:{are}\:{the}\:{two}\:{complex}\:{solution}\:{to} \\ $$$${X}^{−{x}} +\left(−{X}\right)^{{x}} =\mathrm{0}\:{in}\:{addition}\:{to}\:\pm\mathrm{1}\:? \\ $$
Answered by Frix last updated on 16/Feb/23
![x=ri; let r>0 [due to symmetry] (ri)^(−ri) +(−ri)^(ri) =0 2e^((πr)/2) cos (rln r) =0 cos (rln r) =0 rln r =(n−(1/2))π; n∈Z Since the minimum of rln r is −(1/e)≈−.367879 ⇒ n≈.382900 and r∈R ⇒ rln r =(n−(1/2))π; n∈N^★ We get infinite solutions n=1 r≈2.10729948 n=2 r≈3.64417367 n=3 r≈4.92574568 ...](Q187365.png)
$${x}={r}\mathrm{i};\:\mathrm{let}\:{r}>\mathrm{0}\:\left[\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\right] \\ $$$$\left({r}\mathrm{i}\right)^{−{r}\mathrm{i}} +\left(−{r}\mathrm{i}\right)^{{r}\mathrm{i}} =\mathrm{0} \\ $$$$\mathrm{2e}^{\frac{\pi{r}}{\mathrm{2}}} \mathrm{cos}\:\left({r}\mathrm{ln}\:{r}\right)\:=\mathrm{0} \\ $$$$\mathrm{cos}\:\left({r}\mathrm{ln}\:{r}\right)\:=\mathrm{0} \\ $$$${r}\mathrm{ln}\:{r}\:=\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\pi;\:{n}\in\mathbb{Z} \\ $$$$\mathrm{Since}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of}\:{r}\mathrm{ln}\:{r}\:\mathrm{is} \\ $$$$−\frac{\mathrm{1}}{\mathrm{e}}\approx−.\mathrm{367879}\:\Rightarrow\:{n}\approx.\mathrm{382900} \\ $$$$\mathrm{and}\:{r}\in\mathbb{R} \\ $$$$\Rightarrow \\ $$$${r}\mathrm{ln}\:{r}\:=\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\pi;\:{n}\in\mathbb{N}^{\bigstar} \\ $$$$\mathrm{We}\:\mathrm{get}\:\mathrm{infinite}\:\mathrm{solutions} \\ $$$${n}=\mathrm{1}\:{r}\approx\mathrm{2}.\mathrm{10729948} \\ $$$${n}=\mathrm{2}\:{r}\approx\mathrm{3}.\mathrm{64417367} \\ $$$${n}=\mathrm{3}\:{r}\approx\mathrm{4}.\mathrm{92574568} \\ $$$$... \\ $$
Commented by Humble last updated on 16/Feb/23
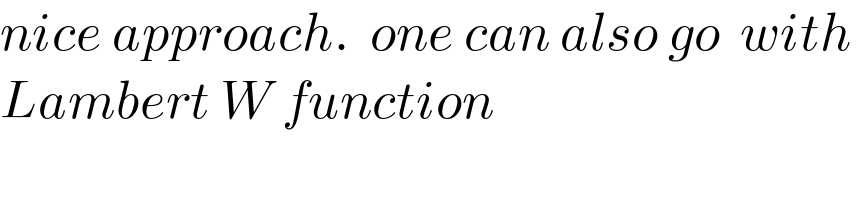
$${nice}\:{approach}.\:\:{one}\:{can}\:{also}\:{go}\:\:{with}\: \\ $$$${Lambert}\:{W}\:{function} \\ $$
