
Question Number 187296 by anurup last updated on 15/Feb/23
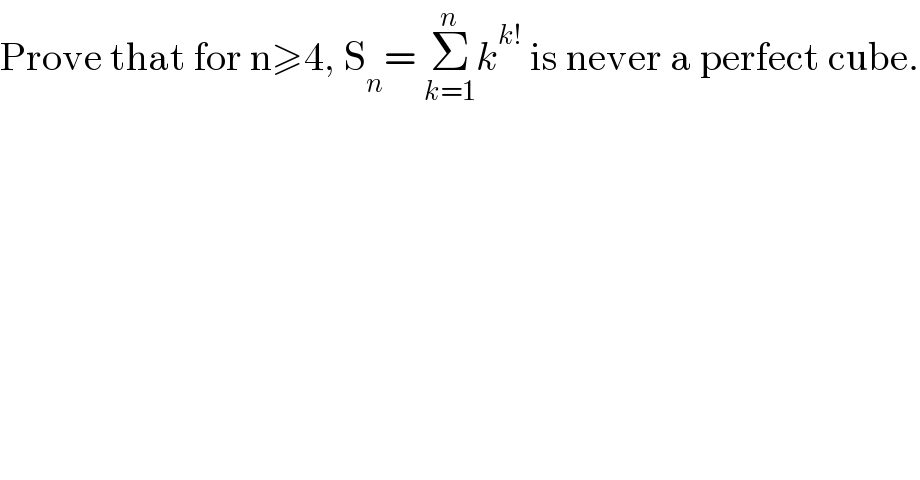
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{for}\:\mathrm{n}\geqslant\mathrm{4},\:\mathrm{S}_{{n}} =\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{{k}!} \:\mathrm{is}\:\mathrm{never}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{cube}. \\ $$
Commented by anurup last updated on 15/Feb/23

$$\mathrm{Please}\:\mathrm{solve}\:\mathrm{this}. \\ $$
