
Question Number 18719 by Tinkutara last updated on 28/Jul/17
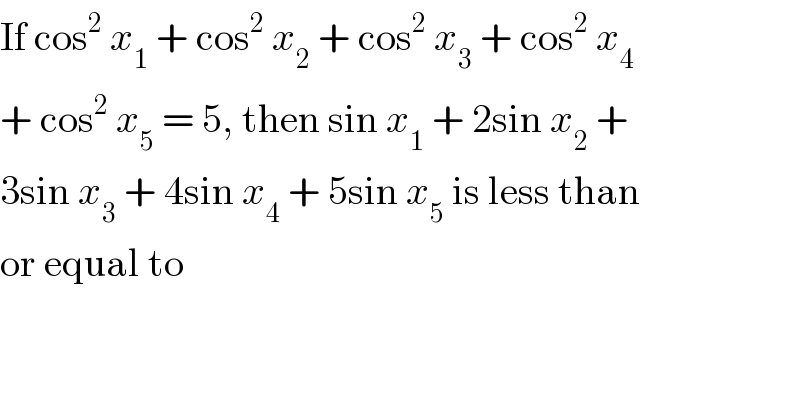
$$\mathrm{If}\:\mathrm{cos}^{\mathrm{2}} \:{x}_{\mathrm{1}} \:+\:\mathrm{cos}^{\mathrm{2}} \:{x}_{\mathrm{2}} \:+\:\mathrm{cos}^{\mathrm{2}} \:{x}_{\mathrm{3}} \:+\:\mathrm{cos}^{\mathrm{2}} \:{x}_{\mathrm{4}} \\ $$$$+\:\mathrm{cos}^{\mathrm{2}} \:{x}_{\mathrm{5}} \:=\:\mathrm{5},\:\mathrm{then}\:\mathrm{sin}\:{x}_{\mathrm{1}} \:+\:\mathrm{2sin}\:{x}_{\mathrm{2}} \:+ \\ $$$$\mathrm{3sin}\:{x}_{\mathrm{3}} \:+\:\mathrm{4sin}\:{x}_{\mathrm{4}} \:+\:\mathrm{5sin}\:{x}_{\mathrm{5}} \:\mathrm{is}\:\mathrm{less}\:\mathrm{than} \\ $$$$\mathrm{or}\:\mathrm{equal}\:\mathrm{to} \\ $$
Commented by mrW1 last updated on 28/Jul/17
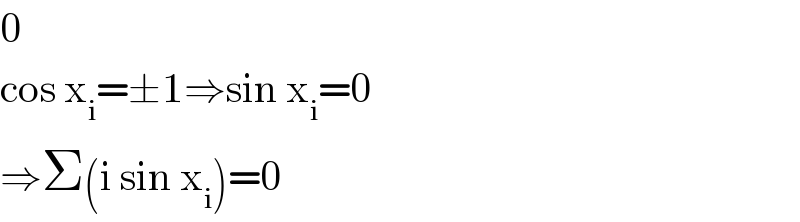
$$\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{x}_{\mathrm{i}} =\pm\mathrm{1}\Rightarrow\mathrm{sin}\:\mathrm{x}_{\mathrm{i}} =\mathrm{0} \\ $$$$\Rightarrow\Sigma\left(\mathrm{i}\:\mathrm{sin}\:\mathrm{x}_{\mathrm{i}} \right)=\mathrm{0} \\ $$
Commented by Tinkutara last updated on 29/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
