
Question Number 187164 by mathlove last updated on 14/Feb/23
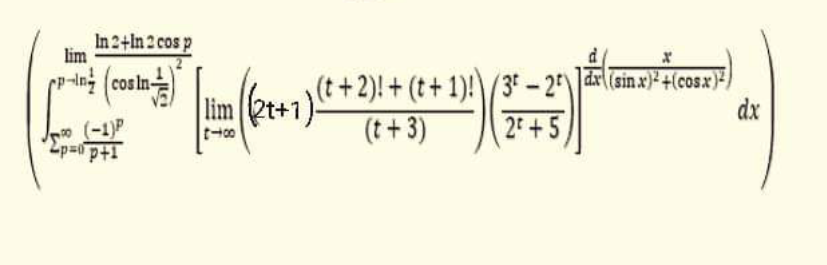
Answered by qaz last updated on 14/Feb/23
![lim_(p→ln(1/2)) ((ln2+ln2 cos p)/((cos ln(1/( (√2))))^2 ))=(((1+cos ln2)ln2)/(cos^2 (1/2)ln2))=(([2cos^2 (1/2)ln2]ln2)/(cos^2 (1/2)ln2))=2ln2 Σ_(p=0) ^∞ (((−1)^p )/(p+1))=Σ_(p=1) ^∞ (((−1)^(p−1) )/p)=ln2 (d/dx)((x/((sin x)^2 +(cos x)^2 )))=(dx/dx)=1 lim_(t→∞) (2t+1)(((t+2)!+(t+1)!)/(t+3))(((3^t −2^t )/(2^t +5))) =lim_(t→∞) (2t+1)(t+1)!∙((1−((2/3))^t )/(((2/3))^t +(5/3^t )))=+∞ I=∫_(ln2) ^(2ln2) (+∞)dx=?](Q187171.png)
$$\underset{{p}\rightarrow{ln}\frac{\mathrm{1}}{\mathrm{2}}} {{lim}}\frac{{ln}\mathrm{2}+{ln}\mathrm{2}\:{cos}\:{p}}{\left({cos}\:{ln}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }=\frac{\left(\mathrm{1}+{cos}\:{ln}\mathrm{2}\right){ln}\mathrm{2}}{{cos}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}}=\frac{\left[\mathrm{2cos}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}\right]{ln}\mathrm{2}}{{cos}^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}}=\mathrm{2}{ln}\mathrm{2} \\ $$$$\underset{{p}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{p}} }{{p}+\mathrm{1}}=\underset{{p}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{p}−\mathrm{1}} }{{p}}={ln}\mathrm{2} \\ $$$$\frac{{d}}{{dx}}\left(\frac{{x}}{\left(\mathrm{sin}\:{x}\right)^{\mathrm{2}} +\left(\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\right)=\frac{{dx}}{{dx}}=\mathrm{1} \\ $$$$\underset{{t}\rightarrow\infty} {{lim}}\left(\mathrm{2}{t}+\mathrm{1}\right)\frac{\left({t}+\mathrm{2}\right)!+\left({t}+\mathrm{1}\right)!}{{t}+\mathrm{3}}\left(\frac{\mathrm{3}^{{t}} −\mathrm{2}^{{t}} }{\mathrm{2}^{{t}} +\mathrm{5}}\right) \\ $$$$=\underset{{t}\rightarrow\infty} {{lim}}\left(\mathrm{2}{t}+\mathrm{1}\right)\left({t}+\mathrm{1}\right)!\centerdot\frac{\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{t}} }{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{t}} +\frac{\mathrm{5}}{\mathrm{3}^{{t}} }}=+\infty \\ $$$${I}=\int_{{ln}\mathrm{2}} ^{\mathrm{2}{ln}\mathrm{2}} \left(+\infty\right){dx}=? \\ $$
