
Question Number 187095 by normans last updated on 13/Feb/23
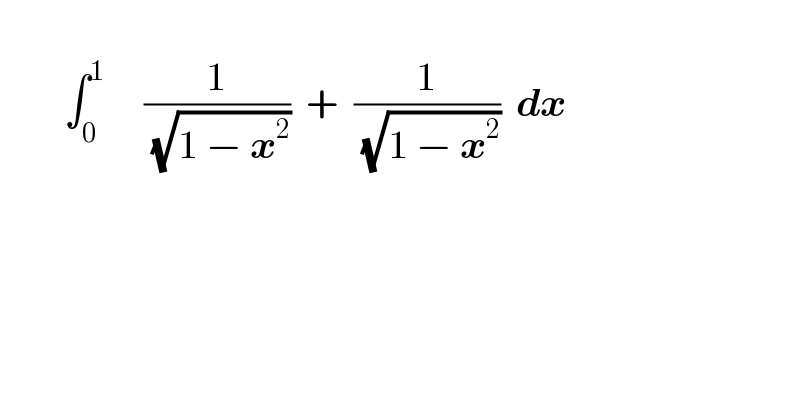
$$ \\ $$$$\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}\:−\:\boldsymbol{{x}}^{\mathrm{2}} }}\:\:+\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}\:−\:\boldsymbol{{x}}^{\mathrm{2}} }}\:\:\boldsymbol{{dx}}\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by Frix last updated on 13/Feb/23
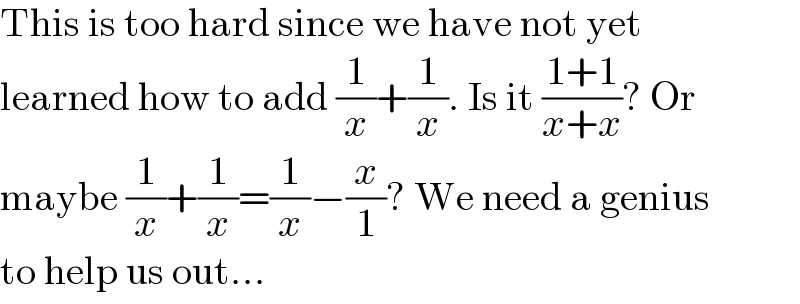
$$\mathrm{This}\:\mathrm{is}\:\mathrm{too}\:\mathrm{hard}\:\mathrm{since}\:\mathrm{we}\:\mathrm{have}\:\mathrm{not}\:\mathrm{yet} \\ $$$$\mathrm{learned}\:\mathrm{how}\:\mathrm{to}\:\mathrm{add}\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}}.\:\mathrm{Is}\:\mathrm{it}\:\frac{\mathrm{1}+\mathrm{1}}{{x}+{x}}?\:\mathrm{Or} \\ $$$$\mathrm{maybe}\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}}=\frac{\mathrm{1}}{{x}}−\frac{{x}}{\mathrm{1}}?\:\mathrm{We}\:\mathrm{need}\:\mathrm{a}\:\mathrm{genius} \\ $$$$\mathrm{to}\:\mathrm{help}\:\mathrm{us}\:\mathrm{out}... \\ $$
Answered by MJS_new last updated on 13/Feb/23

$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is} \\ $$$$−\mathrm{i}\:\mathrm{ln}\:\left(−\mathrm{1}\right) \\ $$
Answered by CElcedricjunior last updated on 14/Feb/23
![∫_0 ^1 ((1/( (√(1−x^2 ))))+(1/( (√(1−x^2 )))))dx=2∫_0 ^1 (dx/( (√(1−x^2 )))) ★Moivre =2[arcsin(x)]_0 ^1 ■cel cedric junior =2[(𝛑/2)] =>∫_0 ^1 ((1/( (√(1−x^2 ))))+(1/( (√(1−x^2 )))))dx=𝛑](Q187225.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}\right)\boldsymbol{{dx}}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{dx}}}{\:\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}\:\bigstar{Moivre} \\ $$$$=\mathrm{2}\left[\boldsymbol{{arcsin}}\left(\boldsymbol{{x}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \blacksquare\boldsymbol{{cel}}\:\:\boldsymbol{{cedric}}\:\boldsymbol{{junior}} \\ $$$$=\mathrm{2}\left[\frac{\boldsymbol{\pi}}{\mathrm{2}}\right] \\ $$$$=>\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }}\right)\boldsymbol{{dx}}=\boldsymbol{\pi} \\ $$
